- Research
- Open access
- Published:
Inclusion Relationship of Uncertain Sets
Journal of Uncertainty Analysis and Applications volume 3, Article number: 13 (2015)
Abstract
Uncertain set is a set-valued function on an uncertainty space, and membership function is used to describe an uncertain set. This paper discusses the inclusion relationship between two uncertain sets and illustrates the relationship via some examples. A formula is derived to calculate the uncertain measure that an uncertain set is included in another one.
Introduction
In order to indicate human’s belief degree on the chance that an event happens, an uncertain measure was defined by Liu [1, 2] as a set function satisfying normality, duality, subadditivity and product axioms. Uncertain set, initialized by Liu [3], is a set-valued function on an uncertainty space to model the unsharp concepts such as “old people” and “heavy vehicles”. In order to describe an uncertain set, a concept of membership function was proposed by Liu [4].
Uncertain sets are the theoretical foundations of uncertain inference control and uncertain logic. In 2010, Liu [3] proposed some inference rules for uncertain systems, which were extended to the rules with multiple antecedents by Gao et al. [5]. Following that, Gao [6] balanced an inverted pendulum by using the uncertain controller. In addition, Peng and Chen [7] showed that the uncertain inference system is a universal approximator. In 2011, Liu [8] applied uncertain set to uncertain logic for dealing with human language by using the truth value formula of uncertain propositions.
The concept of independence for uncertain sets was defined by Liu [9]. Then, the set operational law and arithmetic operational law of independent uncertain sets were given by Liu [4]. The concept of expected value for uncertain set was defined by Liu [3], and formulas to calculate the expected value using the membership function and inverse membership function were given by Liu [10] and Liu [4], respectively. Besides, the variance of uncertain set was proposed by Liu [8] and was investigated by Yang and Gao [11]. In addition, the entropy of uncertain set was presented by Liu [4] and was further studied by Yao and Ke [12], Yao [13], Wang and Ha [14], and Peng and Li [15]. For more details about uncertain sets, please refer to Liu [16] and Yang and Gao [17].
In this paper, we will study the inclusion relationship of uncertain sets. The rest of this paper is organized as follows. The next section is intended to introduce some basic concepts about uncertain sets. Then the inclusion relationship is introduced in Section “Inclusion Relationship”, and a formula to calculate the uncertain measure that an uncertain set is included in another one is derived in Section “Main Results”. Finally, some conclusions are made in Section “Conclusions”.
Preliminary
This section introduces some results about uncertain sets, including the uncertainty space, membership function, independence, and the set operational law.
Definition 1.
(Liu [1]) Let Γ be a nonempty set, and  be a σ-algebra on Γ. A set function
be a σ-algebra on Γ. A set function  is called an uncertain measure if it satisfies the following axioms,
is called an uncertain measure if it satisfies the following axioms,
-
Axiom 1: (Normality)
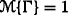
-
Axiom 2: (Duality)
 for any
for any 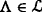 ;
; -
Axiom 3: (Subadditivity) For every sequence of
 we have
we have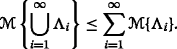
In this case, the triple
 is called an uncertainty space.
is called an uncertainty space.
Besides, a product axiom on the product uncertainty space was given by Liu [ 2 ] for calculating uncertain sets in 2009.
-
Axiom 4: (Product Axiom) Let
 be uncertainty spaces for k=1,2,⋯ Then the product uncertain measure
be uncertainty spaces for k=1,2,⋯ Then the product uncertain measure  is an uncertain measure satisfying
is an uncertain measure satisfying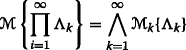
where Λ k are arbitrarily chosen events from
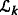 for k=1,2,⋯, respectively.
for k=1,2,⋯, respectively.
Definition 2.
(Liu [3]) An uncertainty set is a measurable function ξ from an uncertainty space  to a collection of sets of real numbers, i.e., for any Borel set B of real numbers, the following two sets
to a collection of sets of real numbers, i.e., for any Borel set B of real numbers, the following two sets
are events.
An uncertain set ξ is called nonempty if  .
.
Definition 3.
(Liu [4]) An uncertain set ξ is said to have a membership function μ if the equations

hold for any Borel set B of real numbers.
Definition 4.
(Liu [9]) The uncertain sets ξ 1,ξ 2,⋯,ξ n are said to be independent if for any Borel sets of real numbers, we have

where \(\xi _{i}^{*}\) are arbitrarily chosen from \(\{\xi _{i},{\xi _{i}^{c}}\},\, i=1,2,\cdots,n,\) respectively.
Theorem 1.
(Liu [4]) Let ξ and η be independent uncertain sets with membership functions μ and ν, respectively. Then the union ξ∪η has a membership function μ(x)∨ν(x), the intersection ξ∩η has a membership function μ(x)∧ν(x), and the complement ξ c has a membership function 1−μ(x).
Inclusion Relationship
In this section, we illustrate the inclusion relationship between uncertain sets via some examples.
Example 1.
Consider an uncertainty space  with
with  and
and  . Define two uncertain sets
. Define two uncertain sets
Then

and

Example 2.
Let ∅ be the empty set, and let ξ be a nonempty uncertain set. Then

and

Example 3.
Let ξ be an uncertain set, and let ℜ be the set of real numbers. Then

Example 4.
Consider an uncertainty space  with Γ={γ
1,γ
2} and
with Γ={γ
1,γ
2} and  and
and  . Define an uncertain set
. Define an uncertain set
Then we have

and

Main Results
In this section, we derive a formula to calculate the uncertain measure that an uncertain set is included in another one.
Theorem 2.
Let ξ and η be two independent uncertain sets with membership functions μ and ν, respectively. Then we have

Proof.
Since
we have

Since ξ∩η c has a membership function μ(x)∧(1−ν(x)), it follows from the definition of membership function that

The theorem is proved.
Remark 1.
To my best knowledge, there is not such a formula in the fuzzy set theory to calculate the possibility measure that a fuzzy set is included in another one.
Example 5.
Let ξ be an uncertain set with a triangular membership function (−4,0,4), and let η be an uncertain set with a trapezoidal membership function (−2,−1,1,2). If ξ and η are independent, then

and

Example 6.
Let ξ be an uncertain set with a membership function μ(x), and B be a Borel set. Note that B can be regarded as an uncertain set with a membership function 1 B (x), and it is independent of the uncertain set ξ. Then according to Theorem 2, we have

and

which coincide with Definition 3 of the membership function.
Example 7.
Let B 1=[1,3] and B 2=[2,4] be two sets of real numbers. Note that they could be regarded as two independent uncertain sets with membership functions \(1_{B_{1}}(x)\) and \(1_{B_{2}}(x)\), respectively. Then we have

and

which coincide with the inclusion relationship of classic sets.
Conclusions
This paper mainly studied the inclusion relationship function of uncertain sets. It gave a formula to calculate the uncertain measure that an uncertain set is included in another one when they are independent.
References
Liu, B: Uncertainty Theory. 2nd edn, Berlin (2007), Springer-Verlag.
Liu, B: Some research problems in uncertainty theory. J. Uncertain Syst. 3(1), 3–10 (2009).
Liu, B: Uncertain set theory and uncertain inference rule with application to uncertain control. J. Uncertain Syst. 4(2), 83–98 (2010).
Liu, B: Membership functions and operational law of uncertain sets. Fuzzy Optim. Decis. Making. 11(4), 387–410 (2012).
Gao, X, Gao, Y, Ralescu, DA: On Liu’s inference rule for uncertain systems. Int. J. Uncertainty Fuzziness Knowledge-Based Syst. 18(1), 1–11 (2010).
Gao, Y: Uncertain inference control for balancing inverted pendulum. Fuzzy Optim. Decis. Making. 11(4), 481–492 (2012).
Peng, Z, Chen, X: Uncertain systems are universal approximators. J. Uncertainty Anal. Appl. 2(13) (2014).
Liu, B: Uncertain logic for modeling human language. J. Uncertain Syst. 5(1), 3–20 (2011).
Liu, B: A new definition of independence of uncertain sets. Fuzzy Optim. Decis. Making. 12(4), 451–461 (2013).
Liu, B: Uncertainty Theory: A branch of mathematics for modeling human uncertainty. Springer-Verlag, Berlin (2010).
Yang, XF, Gao, J: Some results of moments of uncertain set. J. Intel. Fuzzy Syst. 28(6), 2433–2442 (2015).
Yao, K, Ke, H: Entropy operator for membership function of uncertain set. Appl. Math. Comput. 242, 898–906 (2014).
Yao, K: Sine entropy of uncertain set and its applications. Appl. Soft Comput. 22, 432–442 (2014).
Wang, XS, Ha, MH: Quadratic entropy of uncertain sets. Fuzzy Optim. Decis. Making. 12(1), 99–109 (2013).
Peng, J, Li, SG: Radical entropies of uncertain sets. Inf. Int. Interdiscip. J. 16(2A), 895–902 (2013).
Liu, B: Uncertainty Theory. 4th edn. Springer-Verlag, Berlin (2015).
Yang, XF, Gao, J: A review on uncertain set. J. Uncertain Syst. 8(4), 285–300 (2014).
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant No. 61403360).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yao, K. Inclusion Relationship of Uncertain Sets. J. Uncertain. Anal. Appl. 3, 13 (2015). https://doi.org/10.1186/s40467-015-0037-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40467-015-0037-5
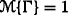
 for any
for any 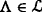 ;
; we have
we have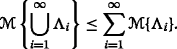
 is called an uncertainty space.
is called an uncertainty space. be uncertainty spaces for k=1,2,
be uncertainty spaces for k=1,2, is an uncertain measure satisfying
is an uncertain measure satisfying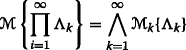
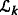 for k=1,2,
for k=1,2,