- Research
- Open access
- Published:
Some moment inequalities for fuzzy martingales and their applications
Journal of Uncertainty Analysis and Applications volume 2, Article number: 7 (2014)
Abstract
Martingales are a class of stochastic processes which has had profound influence on the development of probability theory and stochastic processes. Some recent developments are related to mathematical finance. In the real world, some information about these phenomena might be imprecise and represented in the form of vague quantities. In these situations, we need to generalize classical methods to vague environment. Thus, fuzzy martingales have been extended as a vague perception of real-valued martingales. In this paper, some moment inequalities are presented for fuzzy martingales. Several convergence theorems are established based on these inequalities. As an application of convergence theorems, a weak law of large numbers for fuzzy martingales is stated. Furthermore, a few examples are devoted to clarify the main results.
Introduction
Over the last decades, the theory of fuzzy random variables has been extensively developed. A fuzzy random variable has been extended as a vague perception of a real-valued random variable and subsequently redefined as a particular random set, see e.g., [1–5]. We review several researches on this topic. A strong law of large numbers for fuzzy random variables was given by Miyakoshi and Shimbo [2]. Klement et al. [6] established a strong law of large numbers for fuzzy random variables, based on embedding theorem as well as certain probability techniques in the Banach spaces. Taylor et al. [7] proved a weak law of large numbers for fuzzy random variables in separable Banach spaces. Joo et al. [8] established Chung-type strong law of large numbers for fuzzy random variables based on isomorphic isometric embedding theorem. Fu and Zhang [9] obtained some strong limit theorems for fuzzy random variables with slowly varying weight. It should be mentioned that although the concept of variance has been found very convenient in studying limit theorems, but, as the authors know, the limit theorems for fuzzy random variables based on the concept of variance has not been developed, except in the works by Korner [10] and Feng [11]. Korner [10] proved the strong and weak laws of large numbers for fuzzy random variables. Based on a natural extension of the concept of variance, he extended Kolmogorov’s inequality to independent fuzzy random variables and derived several limit theorems. Their methods are direct applications of classical methods in probability theory to fuzzy random variables. In this paper, some moment inequalities for fuzzy martingales are established and convergence theorems of such fuzzy random variables are studied. We survey some topics in real-valued martingale theory and fuzzy martingale theory. The term martingale originates from the gambling theory. The famous gambling strategy to double one’s stake as long as one loses and leave as soon as one wins is called a martingale. Now, if a gambling value is vague with a certain membership function, the pervious strategy is called fuzzy martingale. A classic interpretation of martingales in the context of gambling is given as follows. Let X n represent the fortune of a gambler at the end of the n th play, and let be the information available to the gambler up to and including the n th play. Then, contains the knowledge of all events like making X n measurable with respect to . The mathematical definition of martingale () says that the given all the information up until the end of the n th play, the expected fortune of the gambler at the end of the (n + 1)th play remains unchanged. Thus, a martingale represents a fair game. In situation where the game puts the gambler in a favorable position, one may express sub-martingale i.e., (). It is mentioned that limit theorems play important roles in studying some practical instances of martingale theory such as extinction in branching process and bankruptcy in investment problems like portfolio selection.
The concept of fuzzy martingale and its properties is introduced and studied by Puri and Ralescu [12], Stojakovic [13], and Feng [14]. Puri and Ralescu [12] proved some convergence theorems of martingale. Stojakovic [13] discussed the properties of martingales. Feng [14] studied fuzzy conditional expectation and fuzzy martingale and investigated some results on convergence of fuzzy martingales. Fei et al. [15] and Fei [16] obtained several results on stopping theorem for fuzzy (super-, sub-) martingales with discrete time.
The rest of this paper is organized as follows. In Section ‘Preliminaries’, we briefly review some preliminary concepts of fuzzy arithmetic and fuzzy random variables. In Section ‘Moment Inequalities’, several useful inequalities are provided for fuzzy martingales. In Section ‘Convergence Theorems’, some limit theorems are established to fuzzy martingales. The conclusions are discussed in Section ‘Conclusions’.
Preliminaries
In this section, we provide several definitions and elementary concepts of fuzzy arithmetic and fuzzy random variables that will be used in the next sections. For more details, the reader is referred to [14, 17, 18].
Define satisfies i to iii }; where (i) is normal, (ii) is fuzzy convex, and (iii) is upper semicontinuous. Any is called a fuzzy number.
For a is called the r-level set of .
We use the notations ⊕, ⊖, and ⊙, which are defined as follows in this paper:
-
(i)
.
-
(ii)
If λ > 0, then .
-
(iii)
If λ < 0, then
-
(iv)
Let and set , where h is the Hausdorff metric, i.e., . Norm of a fuzzy number is defined by , where is the fuzzy number in whose membership function equals 1 at 0 and zero otherwise. The norm ||.|| ∞ of is defined by . The operation is defined by If the indeterminacy of the form ∞ - ∞ arises in the Lebesgue integral, then we say that does not exist. It is easy to see that the operation 〈.,.〉 has the following properties:
-
(i)
.
-
(ii)
.
-
(iii)
.
-
(iv)
.
-
(v)
.
For all if and , then the property (v) implies that . So, we can define In fact, d∗ is a metric in .
Moreover, the norm of fuzzy number is defined by .
Let be a probability space. A fuzzy random variable (briefly, FRV) is a Borel measurable function [14]. Let be a FRV defined on . Then , is a random closed interval, and and are real-valued random variables. A FRV is called integrably bounded if , and the expectation value is defined as the unique fuzzy number which satisfies the property , 0 < r ≤ 1 [3].
Definition 1. ([14]) Let and be two FRVs in L2 ( is FRV and ), then Specially, the variance of is defined by
Theorem 1. ([14]) Letandbe two FRVs in L 2 andand. Then
(i)
(ii)
(iii)
(iv)
(v)
Definition 2. ([19]) The Dp, qdistance, indexed by parameters 1 ≤ p < ∞, 0 ≤ q ≤ 1, between two fuzzy numbers and is a nonnegative function on given as follows:
Remark 1. If , then the metric Dp, qis equal to the metric d∗; for more details, see [16].
To prove the main results, we need to apply an order relation. Thus, we use notations ≺, ≻, ≼, and ≽ defined as follows [18]:
-
(i)
if and only if a - (r) < b - (r) and a + (r) < b + (r) ∀ r ∈ [0,1].
-
(ii)
if and only if a - (r) > b - (r) and a + (r) > b + (r) ∀ r ∈ [0,1].
-
(iii)
if and only if a - (r) ≤ b - (r) and a + (r) ≤ b + (r) ∀ r ∈ [0,1].
-
(iv)
if and only if a - (r) ≥ b - (r) and a + (r) ≥ b + (r) ∀ r ∈ [0,1].
Definition 3. ([20]) Two fuzzy random variables and are called independent if two σ - fields and are independent.
Definition 4. A finite collection of FRVs is said to be independent if σ - fields are independent. An infinite sequence is called independent if every finite sub-collection of it is independent.
Definition 5. ([15]) A fuzzy conditional expectation of with respect to the sub- σ field  of
of  , denoted as , is defined as a FRV which satisfies in the following conditions:
, denoted as , is defined as a FRV which satisfies in the following conditions:
-
(i)
is
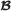 - measurable.
- measurable. -
(ii)
for every . Note that is the Aumann integral of the FRV [21].
Proposition 1. ([15]) The fuzzy conditional expectation has the following properties:
-
(i)
a.s.
-
(ii)
is
 -measurable, then a.s.
-measurable, then a.s. -
(iii)
-
(iv)
If a.s. then a.s.
-
(v)
a.s. and consequently
(1)
Definition 6 ([15]) The sequence of fuzzy random variables and σ - algebras is called a fuzzy martingale if we have, for each n ≥ 1:
-
(a)
is -measurable and
-
(b)
.
The sequence is called a fuzzy sub-martingale if property (b) is replaced by
(b’)
For more on fuzzy martingale and related topics, see e.g. [11, 15, 22].
Definition 7. ([20]) Let and be FRVs defined on the same probability space .
-
(i)
We say that converges to in probability with respect to the metric d if
-
(ii)
We say that converges to almost surely (briefly, a.s.) with respect to the metric d, if
-
(iii)
We say that converges to in L 2 with respect to the metric d, if
It is mentioned that in the literature of probability theory, convergence in probability and almost surely convergence are called weak and strong convergence, respectively.
Throughout the paper, and .
Moment Inequalities
In this section, we prove some basic inequalities for fuzzy martingales.
The following lemma is essential to obtain our main results.
Lemma 1. Ifis a sequence of FRVs such thatfor all n ≥ 1, thenis a fuzzy martingale.
Proof. By using linearity property of conditional fuzzy expectation, we obtain
Since is measurable and we have
This completes the proof.
Corollary 1. Ifis a sequence of independent FRVs such thatthenis a fuzzy martingale.
The above corollary shows the importance of independence in this paper, which is used in the examples.
Remark 2. If is a sequence of fuzzy random variables, then is not always fuzzy martingale.
Example 1. If is a sequence of nonnegative fuzzy random variables, then is not a fuzzy martingale, but it is a fuzzy sub-martingale.
Theorem 2. Ifis a fuzzy martingale, then there exists a constant C depending only on p such that
(i)
(ii)
where,
Proof. We have done the following:
-
(i)
By invoking Fubini’s theorem (FT, for short), Burkholder’s inequality (BI, for short), and C r inequality (C r I, for short), we obtain
-
(ii)
Fubini’s theorem (FT), Rosenthal’s inequality (RI), C r inequality, and conditional Jensen’s inequality (CJI) imply that
It should be noted that the above theorem is a generalization of Theorem 2.11 of [23] to fuzzy martingales.
Now we state and prove two theorems which are extensions of Theorem 2.13 in [23] and Theorem 9.5 of [24], respectively.
Theorem 3. Ifis a fuzzy martingale, then there exists a constant C depending only on p such that
Proof. It is obvious that and constitute ordinary martingales. Also, it is easy to see that
and
By invoking Fubini’s theorem, Burkholder’s inequality, and relations (2) and (3), we obtain
Theorem 4. Ifis a fuzzy martingale and 1 ≤ p ≤ 2, then
Proof. By using monotonicity property of integral (MPI, for short), Fubini’s theorem, Burkholder’s inequality, and C r inequality, we obtain
Convergence Theorems
In this section, by invoking theorems of previous section, we establish some weak and strong convergence theorems for fuzzy martingales.
Theorem 5. Ifis a fuzzy martingale, then
Proof. By invoking Fubini’s theorem and orthogonality lemma of ordinary martingale (OLOM, for short), we obtain
Note that Theorem 5 is a generalization of Lemma 10.4.1 of [24] to fuzzy martingales.
Corollary 2. Ifis a fuzzy martingale such that, thenis Cauchy convergent in L2with respect to the metric d∗.
Lemma 2. Ifis a sequence of FRVs, then
Proof. By using conditional Jensen’s inequality and Fubini’s theorem, we obtain
Corollary 3. Ifis a fuzzy martingale, thenis a real-valued sub-martingale.
Theorem 6. Letbe a fuzzy martingale and p > 2, thenin probability with respect to the metric D p , q if
Proof. By using Markov’s inequality and Theorem 2, the proof is straightforward.
Example 2. Letbe a sequence of independent fuzzy random variables with the following membership functions:
where {X n , n ≥ 1} is a sequence of independent random variables with the following probability
It is easy to see that
where
We want to prove that , i.e., as n → ∞. By using Kronecker’s lemma, it suffices to show that
If , then
By using Theorem 6, we obtainin probability with respect to the metric Dp, qas n → ∞.
The following theorem is an extension of Theorem 2.13 in [23] to fuzzy martingales.
Theorem 7. Letbe a martingale and {b n } be a sequence of positive constants with b n ↑ ∞. Thenin probability with respect to the metric D2, q, if
where, and .
Proof. Suppose that It is easy to see that
We want to prove in probability. By using relation (7), we should prove that (a) and (b) in probability:
-
(a)
For each ε > 0, we have
Thus, in probability.
-
(b)
By using sub-additivity of the metric D 2, q, we obtain
The sub-additivity of the norm ||.||2, q and condition (3) imply that in probability.
It remains to show that in probability.
By using Markov’s inequality and Theorem 3, we have
This completes the proof.
The following example is an evidence of Theorem 7.
Example 3. Suppose thatis a sequence of independent FRVs with the following probability function:
where is a fuzzy number such that It is obvious that
We want to show that
By invoking Markov’s inequality and Lemma 2, we obtain
By using Kronecker’s lemma , and consequently
It remains to show that
It is easy to see that
By invoking Kronecker’s lemma, we obtain and thus,
Therefore, all of the conditions of the above theorem hold, thusin probability with respect to the metric D2, q.
Theorem 8. Letbe a fuzzy martingale. If for all 1 ≤ p < 2,is uniformly integrable, thenas n → ∞.
Proof. By invoking Theorem 2, we obtain
Since is uniformly integrable, by invoking Theorem 5.4.1 in [24] i.e., Hence,
So,
which implies that
The above theorem is a generalization of Theorem 2.22 in [23] to fuzzy martingales.
Example 4. Suppose thatis a sequence of independent Fs with the following probability function:
where is a fuzzy number with the following membership function:
It is easy to see thatis uniformly bounded and, consequently, is uniformly integrable. Thus, by invoking Theorem 8,as n → ∞.
Theorem 9. Ifis a fuzzy martingale such thatfor all p ∈ [1,2], thenconverges almost surely with respect to the metric Dp, q. In particular case,converges almost surely with respect to the metric d ∗ if.
Proof. The completeness of the metric space (E, Dp, q) implies that converges almost surely with respect to the metric Dp, qiff in probability as n → ∞. Let n < m, and consider a Cauchy sequence. Theorem 4 implies that
Now, letting m → ∞, we have
Example 5. Letbe a sequence of independent fuzzy random variables with the following membership functions:
where {X n , n ≥ 1} is a sequence of independent random variables such that Var(X n ) = nβσ2. By considering p = 2 and, we have. For establishing a strong convergence of with respect to the metric Dp, q, it remains to show thatIt is easy to see that, and, where β < - 1. Therefore, Theorem 9 implies thatconverges almost surely with respect to the metric Dp, q.
Conclusions
In this article, we extended some well-known inequalities to fuzzy martingales based on the metric Dp, q. Also, by invoking these inequalities, we established some limit theorems for fuzzy martingales. It is mentioned that if fuzzy random variables reduce to ordinary (real-valued) random variables, all results hold. The study of weak convergence and strong convergence of fuzzy sub-(super-) martingales is a potential topic for future research.
References
Kwakernaak H: Fuzzy random variables I. Inform. Sci 1978, 15: 1–29. 10.1016/0020-0255(78)90019-1
Miyakoshi M, Shimbo M: A strong law of large numbers for fuzzy random variables. Fuzzy Set. Syst 1984, 12: 133–142. 10.1016/0165-0114(84)90033-2
Puri ML, Ralescu DA: Fuzzy random variables. J. Math. Anal. Appl 1986, 114: 402–422.
Puri ML, Ralescu DA: Convergence theorems for fuzzy martingales. J. Math. Anal. Appl 1991, 160: 107–122. 10.1016/0022-247X(91)90293-9
Miranda E, Couso I, Gil P: Random sets as imprecise random variables. J. Math. Anal. Appl 2005, 307: 32–47. 10.1016/j.jmaa.2004.10.022
Klement EP, Puri ML, Ralescu DA: Limit theorems for fuzzy random variables. Proc. Roy. Soc. London Ser. A 1986, 407: 171–182. 10.1098/rspa.1986.0091
Taylor RL, Seymour L, Chen Y: Weak laws of large numbers for fuzzy random sets. Nonlinear Anal 2001, 47: 114–125.
Joo SY, Kim YK, Kwon JS: On Chung’s type law of large numbers for fuzzy random variables. Stat. Probab. Lett 2005, 74: 67–75. 10.1016/j.spl.2005.04.030
Fu K, Zhang L-X: Strong limit theorems for random sets and fuzzy random sets with slowly varying weights. Inform. Sci 2008, 178: 2648–2660. 10.1016/j.ins.2008.01.005
Korner R: On the variance of fuzzy random variables. Fuzzy Set. Syst 1997, 92: 83–93. 10.1016/S0165-0114(96)00169-8
Fei W, Wu R, Shao S: Doob’s stopping theorem for fuzzy (super, sub) martingales with discrete time. Fuzzy Set. Syst 2003, 135: 377–390. 10.1016/S0165-0114(02)00213-0
Ralescu D: Fuzzy random variables revisited. In Mathematics of Fuzzy Sets, Handbook Fuzzy Sets Series, vol. 3. Kluwer, Boston; 1999.
Stojakovic M: Fuzzy martingales-a simple form of fuzzy processes. Stochastic Anal. Appl 1996, 14: 355–367. 10.1080/07362999608809443
Feng Y, Hu L, Shu H: The variance and covariance of fuzzy random variables and their applications. Fuzzy Set. Syst 2001, 120: 487–497. 10.1016/S0165-0114(99)00060-3
Feng Y: Convergence theorems for fuzzy random variables and fuzzy martingales. Fuzzy Set. Syst 1999, 103: 435–441. 10.1016/S0165-0114(97)00180-2
Feng Y: An approach to generalize laws of large numbers for fuzzy random variables. Fuzzy Set. Syst 2002, 128: 237–245. 10.1016/S0165-0114(01)00142-7
Moore RE, Kearfott RB, Cloud MJ: Introduction to Interval Analysis. Siam, Philadelphia; 2009.
Viertl R: Statistical Methods for Fuzzy Data. Chichester, West Sussex: Wiley; 2011.
Sadeghpour Gildeh B, Rahimpour S: A fuzzy bootstrap test for the mean with Dp, q-distance. Fuzzy Inf. Eng 2011, 4: 351–358.
Wu HC: The laws of large numbers for fuzzy random variables. Fuzzy Set. Syst 2000, 116: 245–262. 10.1016/S0165-0114(98)00414-X
Aumann RJ: Integrals of set-valued functions. J. Math. Anal. Appl 1965, 12: 1–12. 10.1016/0022-247X(65)90049-1
Fei W: Regularity and stopping theorem for fuzzy martingales with continuous parameters. Inform. Sci. 2005, 169: 175–187. 10.1016/j.ins.2004.02.011
Hall P, Heyde CC: Martingale Limit Theory and Its Application. New York: Academic; 1980.
Gut A: Probability: a Graduate Course. New York: Springer; 2005.
Acknowledgements
The authors are grateful to referees for their useful and constructive suggestions which lead to an improved version of the paper. The third author would like to thank University of Tehran for partial support of this research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ahmadzade, H., Amini, M., Taheri, S.M. et al. Some moment inequalities for fuzzy martingales and their applications. J. Uncertain. Anal. Appl. 2, 7 (2014). https://doi.org/10.1186/2195-5468-2-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2195-5468-2-7
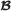 - measurable.
- measurable. -measurable, then a.s.
-measurable, then a.s.