- Research
- Open access
- Published:
Multifactor uncertain differential equation
Journal of Uncertainty Analysis and Applications volume 3, Article number: 7 (2015)
Abstract
This paper proposes a type of multifactor uncertain differential equation within the framework of uncertainty theory. The analytic solutions of four special types of multifactor uncertain differential equations are first discussed. Then, a numerical method for solving general multifactor uncertain differential equation is presented. Finally, under the Lipschitz condition and linear growth condition, it is proved that the multifactor uncertain differential equation has a unique solution.
Introduction
Uncertainty theory is a tool to study the indeterminacy phenomena in human systems, which was founded by Liu [1] in 2007. It was refined by Liu [2] and has become an axiomatic system via normality, duality, subadditivity, and product axioms of uncertain measure. Up to now, many branches of mathematics emerged based on uncertainty theory, such as mathematical programming [3], uncertain set and uncertain inference [4], uncertain logic [5], uncertain risk [6,7], and uncertain insurance [8].
Uncertain process is essentially a sequence of uncertain variables indexed by time which was first introduced by Liu [9]. After that, a significant uncertain process called canonical process was designed by [10]. The canonical process is a stationary independent increment process with Lipschitz continuous sample paths. Meanwhile, uncertain calculus with respect to canonical process called Liu calculus was developed by Liu [10]. In order to describe the evolution of uncertain phenomenon with some jumps, Liu [9] proposed the uncertain renewal process. Afterward, Yao [11] presented the uncertain calculus with respect to renewal process called the Yao calculus. Recently, Yao [12] proposed multi-dimensional uncertain calculus with Liu process, Chen [13] studied the uncertain calculus with finite variation processes. More research about uncertain process can be found in references [14-16].
Uncertain differential equation was proposed by Liu [9], which is an important tool to deal with uncertain dynamic systems. Different from stochastic differential equation driven by a Wiener process [17], uncertain differential equation is a type of differential equation driven by uncertain process. In order to know well uncertain differential equation, many researchers did a lot of work. Chen and Liu [18] proved an existence and uniqueness theorem of solution under global Lipschitz condition and proposed an analytic solution for linear uncertain differential equation. Gao [19] gave an existence and uniqueness theorem with local Lipschitz condition. In 2009, Liu [10] gave a concept of stability of uncertain differential equation. After that, Yao et al. [20] proved some stability theorems of uncertain differential equation. In addition, Sheng and Wang [21] investigated the stability in pth moment for uncertain differential equation, Liu et al. [22] studied the almost sure stability, and Yao et al. [23] showed the stability in mean. In order to obtain the solution of uncertain differential equation, Liu [24] and Yao [25] provided the analytic solutions for some special nonlinear uncertain differential equations, respectively. Yao and Chen [26] presented a numerical method for solving uncertain differential equation when it is difficult to obtain analytic solution. Yao [27] also discussed the extreme values and integral of solution of uncertain differential equation.
Uncertain differential equation was first applied in finance by Liu [10] in 2009. Meanwhile, Liu [10] presented an uncertain stock model in uncertain financial market and proved the European option pricing formulas. After that, Chen [28] gave the America option pricing formulas. Besides, Peng and Yao [29] presented another uncertain stock model and corresponding option pricing formulas. Liu [30] discussed some possible applications of uncertain differential equations to financial markets. Li and Peng [31] proposed a stock model with uncertain stock diffusion. Liu et al. [32] built an uncertain currency model and proved the currency option pricing. Jiao and Yao [33] considered an interest rate model in uncertain environment. Yao [34] proved a no-arbitrage theorem for uncertain stock model. In addition, uncertain differential equation was also applied in uncertain optimal control [35] and uncertain differential game [36].
The extensions of uncertain differential equation also attracted the attention of scholars. Several recent contributions in the extension literature have studied this question in many directions. Yao [11] suggested the uncertain differential equation with jumps. Ge and Zhu [37] discussed the backward uncertain differential equation. Barbacioru [38], Ge and Zhu [39], and Liu and Fei [40] focused on the uncertain delay differential equation. Yao [12] proposed the multidimentional uncertain differential equation via multidimensional uncertain calculus. Ji and Zhou [41] proved an existence and uniqueness theorem of solution for multidimensional uncertain differential equation. Yao [42] studied the higher order uncertain differential equation.
Usually, the uncertain factor influencing dynamic systems is not alone. In 2012, Liu and Yao [43] extended uncertain integral from single canonical process to multiple ones. This provides a motivation to consider the concept of uncertain differential equation driven by multiple uncertain processes. In this paper, we present a type of uncertain differential equation driven by multiple canonical processes which can be regarded as a generalization of the uncertain differential equation proposed by Liu [9].
The rest of the paper is organized as follows. Some preliminary concepts of uncertainty theory and uncertain calculus are recalled in the ‘Preliminary’ section. After that, the multifactor uncertain differential equation is presented. Following that, a numerical method is introduced. In addition, an existence and uniqueness theorem is proved. Finally, a brief summary is given.
Preliminary
In this section, uncertainty theory and uncertain calculus are introduced and some basic concepts are given.
Uncertainty theory
Let Γ be a nonempty set and  a σ-algebra over Γ. Each element Λ in
a σ-algebra over Γ. Each element Λ in  is called an event. A set function
is called an event. A set function 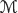 from
from  to [ 0,1] ia called uncertain measure if it satisfies the following axioms:
to [ 0,1] ia called uncertain measure if it satisfies the following axioms:
-
(Normality axiom)
 for the universal set Γ;
for the universal set Γ; -
(Duality axiom)
 for any \(\Lambda \in \mathcal L;\)
for any \(\Lambda \in \mathcal L;\)
-
(Subadditivity axiom) for every countable sequence of events Λ 1,Λ 2,⋯, we have:
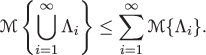
The triplet
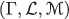 is called an uncertain space. In order to obtain an uncertain measure of compound event, Liu [10] defined a product uncertain measure which produces the fourth axiom of uncertainty theory:
is called an uncertain space. In order to obtain an uncertain measure of compound event, Liu [10] defined a product uncertain measure which produces the fourth axiom of uncertainty theory: -
(Product axiom) Let
 be uncertain spaces for k=1,2,⋯ The product uncertain measure
be uncertain spaces for k=1,2,⋯ The product uncertain measure 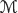 is an uncertain measure on the product σ-algebra \(\mathcal {L}_{1}\times \mathcal {L}_{2} \times \cdots \) satisfying:
is an uncertain measure on the product σ-algebra \(\mathcal {L}_{1}\times \mathcal {L}_{2} \times \cdots \) satisfying:
where Λ k are arbitrarily chosen events from \({\mathcal L}_{k}\) for k=1,2,⋯, respectively.
An uncertain variable is defined as a measurable function from an uncertain space 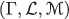 to the set of real numbers, i.e., for any Borel set B of real numbers, the set:
to the set of real numbers, i.e., for any Borel set B of real numbers, the set:
is an event.
The uncertainty distribution Φ:ℜ→[0,1] of an uncertain variable ξ is defined by Liu [1] as:

and the inverse function Φ −1 is called the inverse uncertainty distribution of ξ.
An uncertain variable ξ is called normal if it has a normal uncertainty distribution:
denoted by \({\mathcal N} (e,\sigma \!)\) where e and σ are real numbers with σ>0.
The expected value of uncertain variable ξ is defined by Liu [1] as:

provided that at least one of the two integrals is finite. The variance of ξ is defined as V[ ξ]=E[ (ξ−E[ξ])2].
Let ξ 1,ξ 2,⋯,ξ n be independent uncertain variables with uncertainty distributions Φ 1,Φ 2,⋯,Φ n , respectively. Liu [2] proved that if f(x 1,x 2,⋯,x n ) is a strictly increasing function with respect to x 1,x 2,⋯,x m and strictly decreasing with respect to x m+1,x m+2,⋯,x n , then ξ=f(ξ 1,ξ 2,⋯,ξ n ) is an uncertain variable with inverse uncertainty distribution:
Furthermore, the expected value of uncertain variable ξ=f(ξ 1,ξ 2,⋯,ξ n ) was obtained by Liu and Ha [44] as follows:
Uncertain calculus
Definition 1.
(Liu [9]) Let T be an index set and let 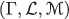 be an uncertain space. An uncertain process is a measurable function from
be an uncertain space. An uncertain process is a measurable function from  to the set of real numbers, i.e., for each t∈T and any Borel set B of real numbers, the set:
to the set of real numbers, i.e., for each t∈T and any Borel set B of real numbers, the set:
is an event.
Definition 2.
(Liu [10]) An uncertain process C t is said to be a canonical process if (i)C 0=0 and almost all sample paths are Lipschitz continuous; (i i)C t has stationary and independent increments; (i i i) every increment C s+t −C t is a normal uncertain variable with expected value 0 and variance t 2.
Definition 3.
(Liu [10]) Let X t be an uncertain process and C t be a canonical process. For any partition of closed integral [ a,b] with a=t 1<t 2<⋯<t k+1=b, the mesh is written as:
Then, Liu integral of X t with respect to C t is:
provided that the limit exists almost surely and is finite. In this case, the uncertain process X t is said to be integrable.
Example 1.
Let f(t) be a continuous function with respect to t. Then, the uncertain integral:
is a normal uncertain variable at each time s, and:
Definition 4.
(Liu [9]) Suppose C t is a canonical process, and f, g are some given functions. Then,
is called an uncertain differential equation.
The uncertain differential with respect to canonical processes C 1t ,C 2t ,⋯,C nt is defined by Liu and Yao [43] as follows.
Definition 5.
(Liu and Yao [43]) Let C 1t ,C 2t ,⋯,C nt be canonical processes and let Z t be an uncertain process. If there exist uncertain processes μ t and σ 1t ,σ 2t ,⋯,σ nt such that:
for any t≥0, then, we say Z t has an uncertain differential:
In this case, Z t is called a differentiable uncertain process with drift μ t and diffusions σ 1t ,σ 2t ,⋯,σ nt .
Theorem 1.
(Liu and Yao [43]) (Fundamental Theorem of Uncertain Calculus) Let C 1t ,C 2t ,⋯,C nt be canonical processes. If h(t,c 1,c 2,⋯,c n ) is a continuously differentiable function, then the uncertain process Z t =h(t,C 1t ,C 2t ,⋯,C nt ) is differentiable and has an uncertain differential:
Multifactor uncertain differential equation
Usually, the uncertain factor influencing dynamic systems is not alone. In order to model the dynamic systems with multiple factors, this section will extend the uncertain differential equation driven by single canonical process to one driven by multiple independent canonical processes.
Definition 6.
(Liu [45]) Uncertain processes X 1t ,X 2t ,⋯,X nt are said to be independent if for any positive integer k and any times t 1,t 1,⋯,t k , the uncertain vectors:
are independent, i.e., for any Borel sets B 1,B 2,⋯,B n of k-dimensional real vectors, we have:

Theorem 2.
(Liu [45]) Let X 1t ,X 2t ,⋯,X nt be independent uncertain processes with regular uncertainty distributions Φ 1t ,Φ 2t ,⋯,Φ nt , respectively. If the function f(x 1,x 2,⋯,x n ) is strictly increasing with respect to x 1,x 2,⋯,x m and strictly decreasing with respect to x m+1,x m+2,⋯,x n , then:
is an uncertain variable with inverse uncertainty distribution:
Definition 7.
Suppose C 1t ,C 2t ,⋯,C nt are independent canonical processes, and f, g 1,g 2,⋯,g n are some given functions. Then:
is called an uncertain differential equation with respect to C 1t ,C 2t ,⋯,C nt . A solution is an uncertain process X t that satisfies Equation 4 identically in t.
The uncertain differential Equation 4 is equivalent to the uncertain integral equation:
Example 2.
Let a, b and c be real numbers, and let C 1t ,C 2t be independent canonical processes. The uncertain differential equation:
has a solution:
Theorem 3.
Let μ t , ν 1t ,ν 2t ,⋯,ν nt be integrable uncertain processes and let C 1t ,C 2t ,⋯,C nt be independent canonical processes. Then, the uncertain differential equation:
has a solution:
Proof. At first, the original uncertain differential equation is equivalent to:
It follows from the fundamental theorem of uncertain calculus that:
and then:
Therefore, the uncertain differential Equation 8 has a solution (9).
Example 3.
Let a, b, and c be real numbers, and let C 1t and C 2t be independent canonical processes. The uncertain differential equation:
has a solution:
Theorem 4.
Let μ 1t , μ 2t , ν 1t ,ν 2t ,⋯,ν nt and ω 1t ,ω 2t ,⋯,ω nt be integrable uncertain processes. Assume C 1t ,C 2t ,⋯,C nt are independent canonical processes, then the uncertain differential equation:
has a solution:
where:
Proof. Define two uncertain processes U t and V t via uncertain differential equations,
It follows from the integration by parts that:
That is, the uncertain process X t =U t V t is a solution of the uncertain differential Equation (12). Note that:
Taking U 0=1 and V 0=X 0, we get the solutions (13) and (14). The theorem is proved.
Note that n=1, the uncertain differential Equation 12 degenerates to the linear uncertain differential equation in Chen and Liu [18].
Example 4.
Let m, a, σ, and ω be real numbers and let C 1t and C 2t be independent canonical processes. The uncertain differential equation:
has the solution:
provided that a≠0.
Example 5.
Let m, σ, and ω be real numbers and let C 1t and C 2t be independent canonical processes. The uncertain differential equation:
has the solution:
Theorem 5.
Let f be a function of two variables and let σ 1t ,σ 2t ,⋯,σ nt be integrable uncertain processes. Assume C 1t ,C 2t ,⋯,C nt are independent canonical processes, then the uncertain differential equation:
has a solution:
where:
and Z t is the solution of uncertain differential equation:
with initial value Z 0=X 0.
Proof. By the fundamental theorem of uncertain calculus, the uncertain process Y t has an uncertain differential:
It follows from the integration by parts that:
That is,
Defining Z t =X t Y t , we obtain \(X_{t}=Y_{t}^{-1}Z_{t}\) and \({dZ}_{t}=Y_{t}f\left (t, Y_{t}^{-1}Z_{t}\right)\). Furthermore, since Y 0=1, the initial value Z 0 is just X 0. The theorem is proved.
Note that n=1, the uncertain differential Equation 19 degenerates to the nonlinear uncertain differential equation in Liu [24].
Example 6.
Let σ 1,σ 2,⋯,σ n be real numbers and let C 1t ,C 2t ,⋯,C nt be independent canonical processes. Consider the uncertain differential equation:
Theorem 5 shows that:
and:
where Z t is the solution of uncertain differential equation:
with initial value Z 0=X 0. Taking \(f(t, X_{t})=X_{t}^{\alpha }\), α≠1, we can obtain:
and:
Theorem 6.
Let g 1,g 2,⋯,g n be functions of two variables and let α t be an integrable uncertain process. Assume C 1t ,C 2t ,⋯,C nt are independent canonical processes, then the uncertain differential equation:
has a solution:
where:
and Z t is the solution of uncertain differential equation:
with initial value Z 0=X 0.
Proof. It follows from the fundamental theorem of uncertain calculus that:
Using the integration by parts, we have the following:
That is,
Define Z t =X t Y t , then \(X_{t}=Y_{t}^{-1}Z_{t}\) and \({dZ}_{t}=Y_{t}\displaystyle \sum \limits _{i=1}^{n}g_{i}\left (t, Y_{t}^{-1}Z_{t}\right){dC}_{\textit {it}}\). In addition, since Y 0=1, the initial value Z 0 is just X 0. The theorem is proved.
Note that n=1, the uncertain differential Equation 24 degenerates to the nonlinear uncertain differential equation in Liu [24].
Example 7.
Let α, b, c, and β be real numbers with β≠1, and let C 1t ,C 2t ,⋯,C nt be independent canonical processes. Consider the uncertain differential equation:
At first,
and Z t satisfies uncertain differential equation:
Since β≠1, we have:
It follows from the fundamental theorem of uncertain calculus that:
Theorem 6 says the uncertain differential equation has a solution:
Numerical method
However, in many cases, it is difficult to find analytic solutions of uncertain differential equations. Yao and Chen [26] presented a numerical method called Yao-Chen method to obtain the inverse uncertainty distribution of solution.
Yao-Chen formula
Definition 8.
(Yao and Chen [26]) Let α be a number with 0<α<1. An uncertain differential equation
is said to have an α-path \(X_{t}^{\alpha }\) if it solves the corresponding ordinary differential equation:
where Φ −1(α) is the inverse standard normal uncertainty distribution, i.e.,
Theorem 7.
(Yao-Chen Formula [26]) Assume that f, g 1,g 2,⋯,g n are continuous functions of two variables. Let X t and \(X_{t}^{\alpha }\) be the solution and α-path of the uncertain differential equation:
respectively. Then:


Theorem 8.
(Yao and Chen [26]) Assume that f, g 1,g 2,⋯,g n are continuous functions of two variables. Let X t and \(X_{t}^{\alpha }\) be the solution and α-path of the uncertain differential equation:
respectively. Then, the solution X t has an inverse uncertainty distribution:
Generalization
In this subsection, we generalize the Yao-Chen formula to the multifactor uncertain differential equation.
Definition 9.
Let α be a number with 0<α<1, and let C 1t ,C 2t ,⋯,C nt be independent canonical processes. An uncertain differential equation:
is said to have an α-path \(X_{t}^{\alpha }\) if it solves the corresponding ordinary differential equation:
where Φ −1(α) is the inverse uncertainty distribution of standard normal uncertain variable \({\mathcal N}(0,1)\), i.e.,
Example 8.
Let a, b, and c be real numbers. The uncertain differential equation:
has an α-path:
Lemma 9.
Assume that f(t,x)and g(t,x) are continuous functions. Let ϕ(t)be a solution of the ordinary differential equation:
where K is a real number. Let ψ(t)be a solution of the ordinary differential equation:
where k(t) is a real function.
-
If k(t)g(t,x)≤K∣g(t,x)∣ for t∈[0,T], then ψ(T)≤ϕ(T),
-
If k(t)g(t,x)>K∣g(t,x)∣ for t∈[0,T], then ψ(T)>ϕ(T).
Theorem 10.
Assume that f, g 1,g 2,⋯,g n are continuous functions of two variables and C 1t ,C 2t ,⋯,C nt are independent canonical processes. Let X t and \(X_{t}^{\alpha }\) be the solution and α-path of the uncertain differential equation:
respectively. Then:


Proof. For each α-path \(X_{t}^{\alpha }\), we construct sets as follows,
i=1,2,⋯,n. It is obvious that \(T_{i}^{+}\cap T_{i}^{-}=\emptyset \) and \(T_{i}^{+}\cup T_{i}^{-}=[0,+\infty)\) for each 1≤i≤n.
Write:
i=1,2,⋯,n, where Φ −1 is the inverse uncertainty distribution of \({\mathcal N}(0, 1)\). Since \(T_{i}^{+}\) and \(T_{i}^{-}\) are disjoint sets and C it have independent increments, we get:

For any \(\gamma \in \Lambda _{i1}^{+}\cap \Lambda _{i1}^{-}\), we always have:
Let \(\Lambda _{1}^{+}\cap \Lambda _{1}^{-}=\displaystyle \bigcap _{i=1}^{n}\left (\Lambda _{i1}^{+}\cap \Lambda _{i1}^{-}\right)\). Because C
1t
,C
2t
,⋯,C
nt
are independent and  , i=1,2,⋯,n, we have:
, i=1,2,⋯,n, we have:

Then, for any \(\gamma \in \Lambda _{1}^{+}\cap \Lambda _{1}^{-}\), we have:
The Lemma 9 shows that \(X_{t}\leq X_{t}^{\alpha }\) for all t, so \(\Lambda _{1}^{+}\cap \Lambda _{1}^{-}\subset \left \{X_{t}\leq X_{t}^{\alpha }, \forall t\right \}\). Hence:

On the other hand, write:
i=1,2,⋯,n. Since \(T_{i}^{+}\) and \(T_{i}^{-}\) are disjoint sets and C it has independent increments, we get:

For any \(\gamma \in \Lambda _{i2}^{+}\cap \Lambda _{i2}^{-}\), we always have:
Let \(\Lambda _{2}^{+}\cap \Lambda _{2}^{-}=\displaystyle \bigcap _{i=1}^{n}\left (\Lambda _{i2}^{+}\cap \Lambda _{i2}^{-}\right)\). Because C
1t
,C
2t
,⋯,C
nt
are independent and  , i=1,2,⋯,n, we have:
, i=1,2,⋯,n, we have:

Then, for any \(\gamma \in \Lambda _{2}^{+}\cap \Lambda _{2}^{-}\), we have:
The Lemma 9 shows that \(X_{t}> X_{t}^{\alpha }\) for any t, so \(\Lambda _{2}^{+}\cap \Lambda _{2}^{-}\subset \left \{X_{t}> X_{t}^{\alpha }, \forall t\right \}\). Hence:

Since \(\left \{X_{t}\leq X_{t}^{\alpha },\forall t\right \}\) and \(\left \{X_{t} \not \leq X_{t}^{\alpha },\forall t\right \}\) are opposite events with each other. It follows from the duality axiom that:

In addition, \(\left \{X_{t}>X_{t}^{\alpha },\forall t\right \} \subset \left \{X_{t} \not \leq X_{t}^{\alpha },\forall t\right \}\) means that:

Thus, the results follow from (33), (34), and (35).
Theorem 11.
Assume that f, g 1,g 2,⋯,g n are continuous functions of two variables and C 1t ,C 2t ,⋯,C nt are independent canonical processes. Let X t and \(X_{t}^{\alpha }\) be the solution and α-path of the uncertain differential equation:
respectively. Then, the solution X t has an inverse uncertainty distribution:
Proof. Obviously, \(\left \{X_{t}\leq X_{t}^{\alpha }\right \}\supset \left \{X_{s} \leq X_{s}^{\alpha },\forall s\right \}\). It follows from the monotonicity theorem and Theorem 10 that:

Similarly, we also obtain:

Besides, by using the duality axiom, we have:

It follows from (36), (37), and (38) that:
Example 9.
Let a, b, and c be real numbers and let C 1t and C 2t be independent canonical processes. The uncertain differential equation:
has a solution:
with an inverse uncertainty distribution:
Based on the previous theorem, the Yao-Chen method can be generalized to the multifactor uncertain differential equation as follows.
-
Fix α on (0,1).
-
Solve the corresponding ordinary differential equation:
$${dX}_{t}^{\alpha}=f\left(t, X_{t}^{\alpha}\right)dt+\sum\limits_{i=1}^{n} \mid g_{i}\left(t, X_{t}^{\alpha}\right)\mid \Phi^{-1}(\alpha)dt $$and obtain \(X_{t}^{\alpha }\), for example, we can choose the recursion formula:
$$X_{i+1}^{\alpha}=X_{i}^{\alpha}+f\left(t_{i}, X_{i}^{\alpha}\right)h+\sum\limits_{j=1}^{n} \mid g_{j}\left(t_{i}, X_{i}^{\alpha}\right)\mid \Phi^{-1}(\alpha)h $$where Φ −1(α) is the inverse standard normal uncertainty distribution and h is the step length.
-
The inverse uncertainty distribution of X t is obtained.
Example 10.
In order to illustrate the numerical method, let us consider an uncertain differential equation:
whose solution is X t = exp(t+C 1t +C 2t ). The Matlab Uncertainty Toolbox (http://orsc.edu.cn/liu/resources.htm) may solve this equation successfully and obtain an inverse uncertainty distribution of X t at t=1/2 shown in Figure 1.
Existence and uniqueness theorem
This section will give an existence and uniqueness theorem of solution for the multifactor uncertain differential equation under Lipschitz condition and linear growth condition.
Lemma 12.
(Chen and Liu [18]) Let C t be a canonical process, and X t an integrable uncertain process on [a,b] with respect to t. Then, the inequality:
holds, where K(γ) is the Lipschitz constant of the sample path X t (γ).
Theorem 13.
Let f, g 1,g 2,⋯,g n be functions of two variables and let C 1t ,C 2t ,⋯,C nt be independent canonical processes. Then, the uncertain differential equation:
has a unique solution if the coefficients f, g 1,g 2,⋯,g n satisfy the Lipschitz condition:
and linear growth condition:
for some constant L. Moreover, the solution is sample-continuous.
Proof. We first prove the existence of solution by a successive approximation method. Define \(X_{t}^{(0)}=X_{0}\), and:
for n=1,2,⋯,n and write:
for each γ∈Γ.
We claim that:
where \(K_{\gamma }=\displaystyle \sum _{i=1}^{n}K_{i\gamma }\), and K i γ is the Lipschitz constant to the sample path C i t (γ), i=1,2,⋯,n.
For n=0, we have:
where the first inequality comes from Lemma 12, the second comes from the linear growth condition.
This confirms the claim for n=0. Next, we assume the claim is true for some n−1. Then:
It follows from Weierstrassąŕ criterion that, for each sample γ, the paths \(X_{t}^{(k)}(\gamma \!)\) converges uniformly on any given interval [0,T]. Write the limit by X t (γ) that is just a solution:
Next, we prove that the solution is unique. Assume that X t and \(X_{t}^{\star }\) are solutions. The Lipschitz condition and linear growth condition show:
It follows from Gronwall inequality that:
Hence, \(X_{t}=X_{t}^{\star }\). The uniqueness is proved.
At last, we will prove the sample-continuity of X t . For each γ∈Γ, by the above proof, we get:
Suppose 0<s<t, we have:
Thus ∣X t (γ)−X s (γ)∣→0 as s→t. Hence, X t is sample-continuous. The theorem is proved.
Note that n=1, the existence and uniqueness theorem degenerates to the one in Chen and Liu [18].
Conclusions
Uncertain differential equation is an important tool to deal with dynamic systems in uncertain environments. In this paper, the multifactor uncertain differential equation was proposed. Four special types of multifactor uncertain differential equations were studied and the corresponding analytic solutions were given. For general multifactor uncertain differential equation, a numerical method was provided for obtaining the solution. Also, an existence and uniqueness theorem that the multifactor uncertain differential equation has a unique solution was proved. The proposed multifactor uncertain differential equation can be used to describe the multifactor stock model in uncertain market.
References
Liu, B: Uncertainty Theory. 2nd ed. Springer-Verlag, Berlin (2007).
Liu, B: Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty. Springer-Verlag, Berlin (2010).
Liu, B: Theory and Practice of Uncertain Programming. 2nd ed. Springer-Verlag, Berlin (2009).
Liu, B: Uncertain set theory and uncertain inference rule with application to uncertain control. J Uncertain Syst. 4(2), 83–98 (2010).
Liu, B: Uncertain logic for modeling human language. J Uncertain Syst. 5(1), 3–20 (2011).
Liu, B: Uncertain risk analysis and uncertain reliability analysis. J. Uncertain Syst. 4(3), 163–170 (2010).
Peng, J: Risk metrics of loss function for uncertain system. Fuzzy Optimization Decis. Making. 12, 53–64 (2013).
Li, S, Peng, J, Zhang, B: The uncertain premium principle based on the distortion function. Insurance:. Math. Econ. 53, 317–324 (2013).
Liu, B: Fuzzy process, hybrid process and uncertain process. J. Uncertain Syst. 2, 3–16 (2008).
Liu, B: Some research problems in uncertainty theory. J. Uncertain Syst. 3, 3–10 (2009).
Yao, K: Uncertain calculus with renewal process. Fuzzy Optimization Decis. Making. 11, 285–297 (2012).
Yao, K: Multi-dimensional uncertain calculus with Liu process. J. Uncertain Syst. 8(4), 244–254 (2014).
Chen, X: Uncertain calculus with finite variation processes (2015).
Gao, Y: Variation analysis of semi-canonical process. Math. Comput. Model. 53, 1983–1989 (2011).
Liu, B: Extreme value theorems of uncertain process with application to insurance risk model. Soft Comput. 17, 549–556 (2013).
Zhang, T, Chen, B: Multi-dimensional canonical process. Information: Int. Interdiscip. J. 16(2A), 1025–1030 (2013).
Itô, K: On stochastic differential equations. Mem. Am. Math. Soc. 4, 1–51 (1951).
Chen, X, Liu, B: Existence and uniqueness theorem for uncertain differential equations. Fuzzy Optimization Decis. Making. 9, 69–81 (2010).
Gao, Y: Existence and uniqueness theorem on uncertain differential equations with local Lipschitz condition. J. Uncertain Syst. 6(3), 223–232 (2012).
Yao, K, Gao, J, Gao, Y: Some stability theorems of uncertain differential equation. Fuzzy Optimization Decis. Making. 12(1), 3–13 (2013).
Sheng, Y, Wang, C: Stability in p-th moment for uncertain differential equation. J. Intell. Fuzzy Syst. 26(3), 1263–1271 (2014).
Liu, H, Ke, H, Fei, Y: Almost sure stability for uncertain differential equation. Fuzzy Optimization Decis. Making. 13(4), 463–473 (2014).
Yao, K, Ke, H, Sheng, Y: Stability in mean for uncertain differential equation (2015).
Liu, Y: An analytic method for solving uncertain differential equations. J. Uncertain Syst. 6, 244–249 (2012).
Yao, K: A type of uncertain differential equations with analytic solution. J. Uncertainty Anal. Appl. 1, Article, 8 (2013).
Yao, K, Chen, X: A numerical method for solving uncertain differential equation. J. Intell. Fuzzy Syst. 25, 825–832 (2013).
Yao, K: Extreme values and integral of solution of uncertain differential equation. J. Uncertainty Anal. Appl. 1, Article, 2 (2013).
Chen, X: American option pricing formula for uncertain financial market. Int. J. Oper. Res. 8, 32–37 (2011).
Peng, J, Yao, K: A new option pricing model for stocks in uncertainty markets. Int. J. Oper. Res. 8, 18–26 (2011).
Liu, B: Toward uncertain finance theory. J. Uncertainty Anal. Appl. 1, Article, 1 (2013).
Li, S, Peng, J: A new stock model for option pricing in uncertain environment. Iran. J. Fuzzy Syst. 11, 27–42 (2014).
Liu, H, Chen, X, Ralescu, D: Uncertain currency model and currency option pricing. Int. J. Intell. Syst. 30(1), 40–51 (2015).
Jiao, D, Yao, K: An interest rate model in uncertain environment (2015).
Yao, K: A no-arbitrage theorem for uncertain stock model. Fuzzy Optimization Decis. Making (2015). doi:10.1007/s10700-014-9198-9.
Zhu, Y: Uncertain optimal control with application to a portfolio selection model. Cybernet. Syst. 41(7), 535–547 (2010).
Yang, X, Gao, J: Uncertain differential games with application to capitalism. J. Uncertainty Anal. Appl. 1, Article, 17 (2013).
Ge, X, Zhu, Y: A necessary condition of optimality for uncertain optimal control problem. Fuzzy Optimization Decis. Making. 12(1), 41–51 (2013).
Barbacioru, I: Uncertainty functional differential equations for finance. Surv. Math. Appl. 5, 275–284 (2010).
Ge, X, Zhu, Y: Existence and uniqueness theorem for uncertain delay differential equations. J. Comput. Inform. Syst. 8(20), 8341–8347 (2012).
Liu, H, Fei, W: Neutral uncertain delay differential equations. Information: Int. Interdiscip. J. 16(2), 1225–1232 (2013).
Ji, X, Zhou, J: Multi-dimensional uncertain differential equation: existence and uniqueness of solution. Fuzzy Optimization Decis. Making (2015). doi:10.1007/s10700-015-9210-z.
Yao, K: Higher order uncertain differential equation. http://orsc.edu.cn/online/141222.pdf (2014).
Liu, B: Yao, K: Uncertain integral with respect to multiple canonical processes. J. Uncertain Syst. 6, 250–255 (2012).
Liu, Y, Ha, M: Expected value of function of uncertain variables. J. Uncertain Syst. 4, 181–186 (2010).
Liu, B: Uncertainty distribution and independence of uncertain processes. Fuzzy Optimization Decis. Making. 13(3), 259–271 (2014).
Acknowledgments
This work is supported by the Projects of the Humanity and Social Science Foundation of Ministry of Education of China (No.13YJA630065), the Key Project of Hubei Provincial Natural Science Foundation (No.2012FFA065).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, S., Peng, J. & Zhang, B. Multifactor uncertain differential equation. J. Uncertain. Anal. Appl. 3, 7 (2015). https://doi.org/10.1186/s40467-015-0031-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40467-015-0031-y
 for the universal set Γ;
for the universal set Γ; for any
for any 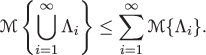
 be uncertain spaces for k=1,2,
be uncertain spaces for k=1,2,
