- Research
- Open access
- Published:
Extraction methods for uncertain inference rules by ant colony optimization
Journal of Uncertainty Analysis and Applications volume 3, Article number: 9 (2015)
Abstract
In recent years, the research on data mining methods has received increasing attention. In this paper, we design an uncertain system with the extracted uncertain inference rules to solve the classification problems in data mining. And then, two extraction methods integrated with ant colony optimization are proposed for the generation of the uncertain inference rules. Finally, two applications are given to verify the effectiveness and superiority of the proposed methods.
Introduction
Nowadays, databases and computer networks, coupled with the use of advanced automated data generation and collection tools, are widely used in many different fields such as finance, E-commerce, logistics, etc. As a result, the amount of data that people have to deal with is dramatically increasing. People hope to carry out scientific research, business decision, or business management on the basis of the analysis of the existing data. However, the current data analysis tools have difficulty in processing the data in depth. To compensate for this deficiency, there come the data mining techniques. Data mining is the computational process of discovering some interesting, potentially useful patterns in large data sets. Those patterns can be concepts, rules, laws, and modes. The overall goal of data mining is to extract information from a data set and transform it into an understandable structure for further use. Data mining helps us to discover valuable information and knowledge. Data mining is applied to many fields in reality. There are many successful examples [1] of data mining in business and science research. For instance, data mining is widely used in financial data analysis, telecommunication, retail, and biomedical research. Therefore, the study of data mining technology has an important practical significance.
The main jobs of data mining are data description, data classification, data dependency, data compartment analysis, data regression, data aggregate, and data prediction. What data classification does is to find a couple of models or functions that can accurately describe the characteristics of the data sets. Then, we can identify the categories of the previously unknown data. After obtaining the models or functions from the set of training data with data mining algorithms, we use many methods to describe the output such as classification rules (if-then), decision trees, mathematical formula, and neutral network.
There are a variety of approaches in data mining. For mining objects in different fields, many different specified methods are invented. The approaches we usually used are statistical methods, machine learning methods, and modern intelligent optimization methods. The statistical methods are very effective methods from the start. In addition, many other data mining methods are invented based on the statistical methods. When dealing with classification problems, Bayesian classification and Bayesian belief network are important classification methods that based on the statistical principle. Machine learning methods are mainly used to solve the conceptual learning, pattern classification, and pattern clustering problems. The core content of machine learning is inductive learning. And there already exist a number of mature technology methods, such as decision tree method for classification problems. Decision trees method is one of the most popular classification methods. The early decision trees algorithm is ID3 method. Later, based on ID3, many algorithms such as C4.5 method [2] are proposed. Besides, there are some variants of the decision trees algorithm including incremental tree structure ID4, ID5, and expandable tree structure SLIQ for massive data set.
In recent years, intelligent optimization algorithms are widely applied into data mining. Neutral network is a simulation model for complex system with nonlinear relations. It is very suitable to deal with complex nonlinear relations in spatial data. Researchers have already proposed different network models to realize the clustering, classification, regression, and pattern recognition of the data. Furthermore, many evolution algorithms such as simulated annealing algorithm are introduced into neutral network algorithm as the optimization strategies. Genetic algorithm is a global search algorithm that simulates the biological evolution and genetic mechanism. It plays an important role in optimization and classification machine learning. Mixed algorithms of genetic algorithm and other algorithms, such as decision trees, neutral network, have been applied to the data mining technology. Ant colony optimization algorithm is a bionic optimization algorithm that simulates the behavior of the ants. Based on that, a data mining technique ant-miner [3] was invented. And Herrera [4] applied it to fuzzy rules learning. However, ant colony optimization algorithm has some weakness such as slow convergence, random initial solutions. For this reason, some improved ant colony optimization algorithms are proposed. Zhu proposed an improved ant colony optimization algorithm (ACOA) [5] and a mutation ant colony optimization algorithm (MACO) [6] to speed up the algorithms and avoid the solutions getting stuck in local optimums. Hybrid genetic ant colony optimization [7] and hybrid particle swarm ant colony optimization algorithm [8] significantly improve the performance of the original ant colony optimization algorithm.
The real world is so complex that human being may face different types of indeterminacy everyday. To get a better understanding of the real world, many mathematical tools are created. One of them is probability theory which is used to model indeterminacy from samples. However, in many cases, no samples are available to estimate a probability distribution. In this situation, we have no choice but to invite some domain experts to evaluate the belief degree that each event may occur. We cannot use probability theory to deal with belief degree since human beings usually overweight unlikely events which makes the belief degrees deviate far from the frequency. In view of this, Liu [9] founded uncertainty theory based on normality axiom, duality axiom, subadditivity axiom, and product measure axiom. It has become a powerful mathematical tool dealing with indeterminacy. Many researchers have done a lot of theoretical work related to uncertainty theory. In 2008, Liu [10] presented the uncertain differential equation. Later, the existence and uniqueness theorem was given [11]. And the stability of uncertain differential equation was discussed [12,13]. Also, some analysis and numerical methods for solving uncertain differential equation were proposed. With uncertain differential equation describing the evolution of the system, we may solve some practical problems. Peng and Yao [14] studied an option pricing models for stocks. Zhu [15] proposed an uncertain optimal control model in 2010.
In [16,17], Liu proposed and studied the uncertain systems based on the concepts of uncertain sets, membership functions, and uncertain inference rules. An uncertain system is a function from its inputs to outputs based on the uncertain inference rule. Usually, an uncertain system consists of five parts: inputs, rule-base, uncertain inference rules, expected value operator, and outputs. Following that, Gao et al. [18] generalized uncertain inference rules and described uncertain systems with them. Peng and Chen [19] proved that uncertain systems are universal approximator and then demonstrated that the uncertain controller is a reasonable tool. Gao [20] designed an uncertain inference controller that successfully balanced an inverted pendulum with 5×5 if-then rules. What is more important is that this uncertain inference controller has a good ability of robustness.
On the basis of uncertainty theory, we consider two extraction methods for uncertain inference rules by ant colony optimization algorithm. In the next section, we review the ant colony optimization algorithm and give some basic concepts about uncertain sets. Then, we formulate a model to extract inference rules based on data set. And then, we propose an extraction method for uncertain inference rules by ant colony optimization algorithm with a mutation operation. Finally, we combine the ant colony optimization algorithm with simulated annealing algorithm to speed up the extraction method. In the last section, we discuss two typical classification problems in data mining with our results.
Preliminary
In this section, we review the ant colony optimization algorithm. And then, we give some basic concepts on uncertainty sets.
Ant colony optimization algorithm
Ant colony optimization algorithm, initiated by Dorigo, is a heuristic optimization approach. It simulates the behavior of real ants when they forage for food which relies on the pheromone communication. In ant colony optimization algorithm, each path of artificial ants walking from the food sources to the nest is a candidate solution to the problem. When walking on the path, the ants will release pheromone which evaporates over time. And the artificial ants will lay down more pheromone on the path corresponding to the better solution. While one ant has many paths to go, it will make a choice according to the amount of the pheromone on the paths. The more pheromone there is on the path, the better the solution is. As a result, bad paths will disappear since the pheromone evaporates over time. And good paths will be reserved since ants walking on it increases the pheromone levels. Finally, one path which is used by most of the ants is left. Then, the optimal solution to the problem is obtained.
Consider the following optimization problem:
where x is the decision variable in the domain D. And f(x) is the objective function while g(x) is the constraint function.
We can use ant colony optimization algorithm to obtain the optimal solution to the problem (1). The parameters in the algorithm are initial pheromone τ 0, ant transfer probability p, number of ants M, pheromone evaporation rate ρ, and number of iterations T. The procedures are as follows. Step 1 Randomly generate a feasible solution x 0 and set optimal solution s=x 0. Initialize all pheromone trails with the same pheromone level τ 0. Set k←0. Step 2 The artificial ant generates a walking path x in some probability p according to the pheromone trails. If x∈D, then go to Step 3; otherwise, repeat Step 2 until x∈D. Step 3 Repeat Step 2 until for each ant and generate M feasible solutions. Let s k be the best solution in this iteration. Step 4 If f(s k )<f(s), then s←s k and update the pheromone trails according to the optimal solution in the current iteration. Step 5 If k<T, then k←k+1 and go to Step 2; otherwise, terminate. Step 6 Report the optimal solution.
Uncertain set
Let Γ be a nonempty set and  be σ-algebra over Γ. Each \(\Lambda \in \mathcal {L}\) is called an event. For any Λ,
be σ-algebra over Γ. Each \(\Lambda \in \mathcal {L}\) is called an event. For any Λ,  . The set function
. The set function  defined on
defined on  is called an uncertain measure if it satisfies the following three axiom:
is called an uncertain measure if it satisfies the following three axiom:  for any
for any  for all \(\Lambda _{1}, \Lambda _{2},\cdots \in \mathcal {L}\). Then, the triplet
for all \(\Lambda _{1}, \Lambda _{2},\cdots \in \mathcal {L}\). Then, the triplet  is called an uncertainty space [9]. The product uncertain measure
is called an uncertainty space [9]. The product uncertain measure  is an uncertain measure satisfying
is an uncertain measure satisfying  , where Λ
k
are arbitrarily chosen events from \(\mathcal {L}_{k}\) for k=1,2,⋯, respectively.
, where Λ
k
are arbitrarily chosen events from \(\mathcal {L}_{k}\) for k=1,2,⋯, respectively.
Definition 1.
[
16
] An uncertain set is a function ξ from an uncertainty space  to a collection of sets of real numbers such that both {B⊂ξ} and {ξ⊂B} are events for any Borel set B.
to a collection of sets of real numbers such that both {B⊂ξ} and {ξ⊂B} are events for any Borel set B.
Example 1.
Take  to be {γ
1,γ
2,γ
3} with power set
to be {γ
1,γ
2,γ
3} with power set  . Then, the set-valued function
. Then, the set-valued function
is an uncertain set on  .
.
Definition 2.
[ 16 ] The uncertain sets ξ 1,ξ 2,ξ 3,⋯,ξ n are said to be independent if for any Borel sets B 1,B 2,B 3,⋯,B n , we have

and

where \(\xi _{i}^{*}\) are arbitrarily chosen from \(\left \{\xi _{i}, {\xi _{i}^{c}}\right \}\), i=1,2,⋯,n, respectively.
Definition 3.
[ 21 ] An uncertain set ξ is said to have a membership function μ if for any Borel set B of real numbers, we have

The above equations will be called measures inversion formulas.
Remark 1.
When an uncertain set ξ does have a membership function μ, it follows from the first measure inversion formula that

Example 2.
An uncertain set ξ is called triangular if it has a membership function
denoted by (a,b,c) where a,b,c are real numbers with a<b<c.
Definition 4.
[ 21 ] A membership function μ is said to be regular if there exists a point x 0 such that μ(x 0)=1, and μ(x) is unimodal about the mode x 0. That is, μ(x) is increasing on (−∞,x 0] and decreasing on [x 0,+∞).
Definition 5.
[ 16 ] Let ξ be an uncertain set. Then, the expected value of ξ is defined by

provided that at least one of the two integrals is finite and

Theorem 1.
[ 13 ] Let ξ be an uncertain set with regular membership function μ. Then
where x 0 is a point such that μ(x 0)=1.
Example 3.
Let ξ be a triangular uncertain set denoted by (a,b,c). Then, according to Theorem 1, we have
In fact, it follows from Equations 2 and 3 that
Uncertain inference rule
Here, we introduce concepts of the uncertain inference and uncertain system. Inference rules are the key points of the inference systems. In fuzzy systems, CRI approach [22], Mamdani inference rules [23] and Takagi-Sugeno inference rules [24] are the most common used inference rules. Fuzzy if-then inference rules use fuzzy sets to describe the antecedents and the consequents. Unlike fuzzy inference, both antecedents and consequents in uncertain inference are characterized by uncertain sets. Uncertain inference [16] is a process of deriving consequences from human knowledge via uncertain set theory. First, we introduce the following inference rule.
Inference Rule 1.
[16] Let  and
and  be two concepts. Assume a rule ‘if
be two concepts. Assume a rule ‘if  is an uncertain set ξ, then
is an uncertain set ξ, then  is an uncertain set η’. From
is an uncertain set η’. From  is a constant a, we infer that
is a constant a, we infer that  is an uncertain set
is an uncertain set
which is the conditional uncertain set of η given a∈ξ. The inference rule is represented by
-
Rule: If
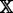 is ξ, then
is ξ, then 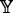 is η
is η
-
From:
 is a constant a
is a constant a -
Infer:
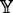 is η
∗=η|
a∈ξ
is η
∗=η|
a∈ξ
Theorem 2.
[ 16 ] Let ξ and η be independent uncertain sets with membership functions μ and ν, respectively. If ξ ∗ is a constant a, then the Inference Rule 1 yields that η ∗ has a membership function
Based on Inference Rule 1, Gao et al. [18] proposed the multi-input, multi-if-then-rule inference rules.
Inference Rule 2.
[13] Let \(\mathbb {X}_{1}, \mathbb {X}_{2}, \cdots, \mathbb {X}_{m}, \mathbb {Y}\) be concepts. Assume rules ‘if \(\mathbb {X}_{1}\) is ξ
i1 and ⋯ and \(\mathbb {X}_{m}\) is ξ
im
, then  is η
i
’ for i=1,2,⋯,k. From \(\mathbb {X}_{1}\) is a constant a
1 and ⋯ and \(\mathbb {X}_{m}\) is a constant a
m
, we infer that
is η
i
’ for i=1,2,⋯,k. From \(\mathbb {X}_{1}\) is a constant a
1 and ⋯ and \(\mathbb {X}_{m}\) is a constant a
m
, we infer that
where the coefficients are determined by

for i=1,2,⋯,k. The inference rule is represented by
-
Rule 1: If \(\mathbb {X}_{1}\) is ξ 11 and ⋯ and \(\mathbb {X}_{m}\) is ξ 1m , then
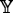 is η
1
is η
1
-
Rule 2: If \(\mathbb {X}_{1}\) is ξ 21 and ⋯ and \(\mathbb {X}_{m}\) is ξ 2m , then
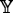 is η
2
is η
2
-
⋯
-
Rule k: If \(\mathbb {X}_{1}\) is ξ k1 and ⋯ and \(\mathbb {X}_{m}\) is ξ km , then
 is η
k
is η
k
-
From: \(\mathbb {X}_{1}\) is a 1 and ⋯ and \(\mathbb {X}_{m}\) is a m
-
Infer:
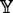 is determined by Eq. (4)
is determined by Eq. (4)
Theorem 3.
[13] Assume ξ i1,ξ i2,⋯,ξ im ,η i are independent uncertain sets with membership functions μ i1,μ i2,⋯,μ im ,ν i , i=1,2,⋯,k, respectively. If \(\xi _{1}^{*}, \xi _{2}^{*}, \cdots, \xi _{m}^{*}\) are constants a 1,a 2,⋯,a m , respectively, then the Inference Rule 2 yields
where \(\eta _{i}^{*}\) are uncertain sets whose membership functions are given by
and \(c_{i}=\min \limits _{1\leq l\leq m}\mu _{\textit {il}}(a_{l})\) are constants.
Uncertain system
Uncertain system, proposed by Liu [16], is a function from its inputs to outputs based on the uncertain inference rule. Usually, an uncertain system consists of five parts: inputs that are crisp data to be fed into the uncertain system; a rule-base that contains a set of if-then rules provided by the experts; an uncertain inference rule that infers uncertain consequents from the uncertain antecedents; an expected value operator that converts the uncertain consequents to crisp values; and outputs that are crisp data yielded from the expected value operator.
Now, we consider an uncertain system with m crisp inputs α 1,α 2,⋯,α m , and n crisp outputs β 1,β 2,⋯,β n . We have the following if-then rules:
-
If \(\mathbb {X}_{1}\) is ξ 11 and ⋯ and \(\mathbb {X}_{m}\) is ξ 1m , then \(\mathbb {Y}_{1}\) is η 11 and \(\mathbb {Y}_{2}\) is η 12 and ⋯ and \(\mathbb {Y}_{n}\) is η 1n
-
If \(\mathbb {X}_{1}\) is ξ 21 and ⋯ and \(\mathbb {X}_{m}\) is ξ 2m , then \(\mathbb {Y}_{1}\) is η 21 and \(\mathbb {Y}_{2}\) is η 22 and ⋯ and \(\mathbb {Y}_{n}\) is η 2n
-
⋯
-
If \(\mathbb {X}_{1}\) is ξ k1 and ⋯ and \(\mathbb {X}_{m}\) is ξ km , then \(\mathbb {Y}_{1}\) is η k1 and \(\mathbb {Y}_{2}\) is η k2 and ⋯ and \(\mathbb {Y}_{n}\) is η kn
Thus, according to Inference Rule 1 and 2, we can infer that \(\mathbb {Y}_{j}(j=1, 2, \cdots, n)\) are
where  for i=1,2,⋯,k. Then, by using the expected value operator, we obtain
for i=1,2,⋯,k. Then, by using the expected value operator, we obtain
for j=1,2,⋯,n. Now, we construct a function from crisp inputs α 1,α 2,⋯,α m to crisp outputs β 1,β 2,⋯,β n , i.e.,
Then, we get an uncertain system f. For the uncertain system we proposed, we have the following theorem.
Theorem 4.
[ 13 ] Assume that ξ i1,ξ i2,⋯,ξ im and η i1,η i2,⋯,η in are independent uncertain sets with membership functions μ i1,μ i2,⋯,μ im ,ν i1,ν i2,⋯,ν in , i=1,2,⋯,k, respectively. Then, the uncertain system from α 1,α 2,⋯,α m to β 1,β 2,⋯,β n is
where j=1,2,⋯,n and \(\eta _{\textit {ij}}^{*}\) are uncertain sets whose membership functions are given by
and \(c_{i}=\min \limits _{1\leq l\leq m}\mu _{\textit {il}}(a_{l})\) are constants.
Next, we discuss the expected value of a special triangular uncertain set. Without loss of generality, we assume n=1. Then the uncertain system proposed in the above becomes:
Theorem 5.
Assume we have an uncertain system with m inputs and 1 output consisting of k inference rules. The antecedents of the rules are represented by the uncertain sets ξ i with membership functions μ i1,μ i2,⋯,μ im ,i=1,2,⋯,k. And the consequent is represented by an triangular uncertain set η i =(α i ,β i ,γ i ) with a membership function ν i , where the coefficients satisfy
We have
Proof.
Given the m input data a 1,a 2,⋯,a m , we can calculate c i from Equation 7. Then, we can get the membership functions \(\nu _{i}^{*}\) of the consequence uncertain sets \(\eta _{i}^{*}\) according to Equation 6. Next, the computation of the expected value of uncertain consequence breaks into three cases.
Case 1: Assume c i /2=0.5. We can immediately have \(\nu _{i}^{*}(y)=\nu _{i}(y)\), thus
Case 2: Assume c i /2<0.5. Let \(y_{11}^{i}\) and \(y_{12}^{i} \left (y_{11}^{i}<y_{12}^{i}\right)\) be the two points that satisfy the equation ν i (y)=c i /2. Similarly, \(y_{21}^{i}\) and \(y_{22}^{i} \left (y_{21}^{i}<y_{22}^{i}\right)\) satisfy the equation ν i (y)=1−c i /2. Since the membership function of a triangular uncertain set has a symmetry property, we have
Then, we can rewrite the membership function of η i as follows:
And \(\nu _{i}^{*}(\beta _{i})=1\). Together with Equations 3, 8, and 9, we have
Case 3: Assume c i >0.5. Similarly, we have \(E[\eta _{i}^{*}]=\beta _{i}\). Thus, we have proved the theorem. □
Problem formulation
In this section, we propose an extraction model to obtain uncertain inference rules.
Let X=(x 1,x 2,⋯,x n ) be the decision vector, which represents a rule base consisting of n rules. Each rule has m antecedents which are described by Q uncertain sets and one consequent which is described by R uncertain sets. Each variable x i represents a sequence x i1 x i2⋯x im x i m+1, where x ij ∈{0,1,2,⋯,Q}(i=1,2,⋯,n;j=1,2,⋯,m) represent the antecedents of the inference rule. And x i m+1∈{0,1,2,⋯,R}(i=1,2,⋯,n) represent the consequent. Thus, each variable of decision vector represents one inference rule. Some x ij =0 means this antecedent is not included. And some x i m+1=0 means this inference rule will not be included in the rule base. For example, assume that we have one inference rule consists of 4 antecedents and 1 consequent. They are described by 5 uncertain sets which refer to five descriptions: very low, low, medium, high, and very high. We use 1,2,3,4,5 to denote them. Thus, sequence “23045”, for example, represents the rule: “if input 1 is low, input 2 is medium, and input 4 is high, then the output is very high”.
Uncertain systems can be used for classification. But which uncertain system is better depends on the rule base. Here, we try to find best rule base by comparing the mean absolute errors of the origin output and the system output. That is,
where P is the number of training data, o i ,t i (i=1,2,⋯,P) are the system outputs and origin outputs, respectively. If we find the rule base with the least mean absolute error, we extract the uncertain inference rules successfully. We can obtain the system outputs by Equation 5. However, they may not be integers. To avoid this nonsense, for a classification problem with C classes, we can divide interval that covers all the system outputs into C subintervals. Then, if the output from Equation 5 is in the ith subinterval, we have o i =i. Thus, we transfer the classification problem to the following optimization model:
Extraction method for uncertain inference rules with mutations
In this section, we propose the extraction method for uncertain inference rules with mutations by ant colony optimization algorithm.
As stated before, each x i is a sequence of m values in {0,1,2,⋯,Q} and 1 value in {0,1,2,⋯,R}. Without loss of generality, we set Q=R. Each number in {0,1,2,⋯,Q} is a node. Let ants walking across these nodes. Ants choose the next node in probability based on the pheromone levels in the Q+1 choices at every step. Once ants move m+1 steps, a candidate decision variable is generated. After repeat this process n times, we get a candidate solution. After all ants finish their walk, update the pheromone trails. Denote the pheromone trail by τ i;k,j (t) associated to the node j at step k of x i in iteration t. The procedures are described as follows. (1) Initialization: Randomly generate a feasible solution X 0, and set the optimal solution \(\hat {X}=X_{0}\). Set τ i;k,j (0)=τ 0, i=1,2,⋯,n, k=1,2,⋯,m+1, j=0,1,2,⋯,Q, where τ 0 is a fixed parameter. (2) Ant movement: At each step k after building the sequence x i1 x i2⋯x ik , select the next node in probability following
In this way, we could get a sequence x i1 x i2⋯x i m+1. To speed up the algorithm, we mutate this sequence to get a new candidate sequence. The mutation is made as follows: randomly add 1 or subtract 1 to each element x ij in the sequence; if the element is 0, the mutated element is 1; if the element is Q, the mutated element is Q−1. Assume X ′ is the mutated solution, if Δ F=F(X ′)−F(X)≤0, then X←X ′; otherwise, keep the current solution. If Q is very large, we could repeat this mutation until some termination condition is satisfied. (3) Pheromone Update: At each iteration t, let \(\hat {X}\) be the optimal solution found so far and X t be the best feasible solution in the current iteration. Assume \(F(\hat {X})\) and F(X t ) are the corresponding objective function values.
If \(F(X_{t})<F(\hat {X})\), then \(\hat {X}\leftarrow X_{t}\).
Reinforce the pheromone trails on nodes of \(\hat {X}\) and evaporate the pheromone trails on the left nodes:
where ρ(0<ρ<1) is the evaporation rate, g(x)(0<g(x)<+∞) is a function with that g(x)≥g(y) if F(x)<F(y), for example, g(x)=L/(|F(x)|+1) is a function satisfying the condition where L>0.
Let τ 0 be the initial value of pheromone trails, n be the number of decision variables, M be the number of ants, ρ be evaporation rate and T be the number of iterations. Now, we summarize the algorithm as follows. Step 1 Initialize all pheromone trails with the same pheromone level τ 0. Randomly generate a feasible solution X 0, and set optimal solution \(\hat {X}=X_{0}\). Set l←0. Step 2 Ant movement in probability following Equation 12. Generate a decision variable x i after m+1 steps. Step 3 Repeat Step 2 until X=(x 1,x 2,⋯,x n ) is generated; mutate every x i : thus, generate a new decision vector \(X^{\prime }=(x_{1}^{\prime },x_{2}^{\prime },\cdots,x_{n}^{\prime })\); if Δ F=F(X ′)−F(X)≤0, then X←X ′. Step 4 Repeat Step 2 and Step 3 for all M ants. Step 5 Calculate the system outputs by Equation 5. Then, calculate the objective function values for the M candidate solutions by Equation 11. Denote the best solution in this iteration by X l . Step 6 If \(F(X_{l})<F(\hat {X})\), then \(\hat {X}\leftarrow X_{l}\); update the pheromone trails according to Equation 13. Step 7 l←l+1; if l=T, terminate; otherwise, go to Step 2. Step 8 Report the optimal solution \(\hat {X}\).
With this algorithm above, we obtain an uncertain rule base. Then, we successfully design an uncertain system and can use it for classification.
Extraction method for uncertain inference rules with SA
In the previous section, to speed up the algorithm, we introduce a mutation operation. Here, we introduce the simulated annealing algorithm as the local search operation.
Simulated annealing algorithm was initiated by Metropolis in 1953, applied to portfolio optimization by Kirkpatrick [25] in 1983. The name and inspiration come from annealing in metallurgy, a technique involving heating and controlled cooling of a material to increase the size of its crystals and reduce their defects. Simulated annealing algorithm is excellent at avoiding getting stuck in local optimums. It has a good robust property and is universal and easy to implement.
For optimization problem (1), we can use simulated annealing algorithm to search for the optimal solution. The algorithm is as follows. Step 1 Randomly generate a initial solution x 0; x←x 0; k←0; t 0←t max (initial temperature); Step 2 If the temperature satisfies the inner cycle termination criterion, go to Step 3; otherwise, randomly choose a point x ′ in the neighborhood N(x), calculate Δ f=f(x ′)−f(x). If Δ f≤0, then x←x ′; otherwise, according to Metropolis acceptance criterion, if exp(−Δ f/t k )>r a n d o m(0,1), then x←x ′. Repeat Step 2. Step 3 t k+1=d(t k ) (temperature decrease); k←k+1; if the termination criterion is satisfied, stop and report the optimal solution; otherwise, go to Step 2.
In this section, we combine ant colony optimization algorithm and simulated annealing algorithm. In each iteration of ant colony optimization algorithm, we get a feasible solution. Then, we use it as the initial solution of the simulated annealing algorithm to get a neighbor solution. This neighbor solution will be accepted in probability. And for each decision vector X=(x 1,x 2,⋯,x n ), x i =x i1 x i2⋯x i m+1, we build the neighbor solution as follows: for each x i , for some randomly generated p and q (1≤p<q≤m), reverse the order of the sequence x ip ⋯x iq , i.e., \(x_{i}^{\prime }=x_{i1}\cdots x_{ip-1}x_{\textit {iq}}x_{iq-1}\cdots x_{ip+1}x_{\textit {ip}}x_{iq+1}\cdots x_{im+1}\). For example, assume x i is 0123456, p=2, q=6, and the neighbor solution \(x_{i}^{\prime }\) is 0543216. In this way, we obtain a neighbor solution X ′. If Δ F=F(X ′)−F(X)≤0, X←X ′; otherwise, if exp(−Δ F/t k )>r a n d o m(0,1), then X←X ′; otherwise, abandon this neighbor solution. Still denote the pheromone trail by τ i;k,j (t). The procedure are described as follows. (1) Initialization: Generate a feasible solution X 0 randomly and set the optimal solution \(\hat {X}=X_{0}\). Set τ i;k,j (0)=τ 0, i=1,2,⋯,n, k=1,2,⋯,m+1, j=0,1,2,⋯,Q, where τ 0 is a fixed parameter. (2) Ant movement: At each step k after building the sequence x i1 x i2⋯x ik , select the next node in probability following Equation 12. In this way, we could get a sequence x i1 x i2⋯x i m+1. In order to expand the search range, we use simulated annealing algorithm to search locally around the solution at this step. Assume the neighbor solution is X ′. If Δ F=F(X ′)−F(X)≤0, X←X ′; otherwise, if exp(−Δ F/t k )>r a n d o m(0,1) where t k is the current temperature and t k →0 when k→∞, then X←X ′; otherwise, abandon this neighbor solution and still choose the original feasible solution. (3) Pheromone Update: Let \(\hat {X}\) be the optimal solution found so far and X t be the best feasible solution in the current iteration t. Assume \(F(\hat {X})\) and F(X t ) are the corresponding objective function values. To avoid the optimal solution \(\hat {X}\) getting stuck in local optimums, we also use acceptance function here.
If \(F(X_{t})< F(\hat {X})\), then \(\hat {X}\leftarrow X_{t}\).
Build a neighbor solution \(\hat {X}^{\prime }\).
If \(F(\hat {X}^{\prime })\leq F(\hat {X})\), then \(\hat {X}\leftarrow \hat {X}^{\prime }\);
If \(F(\hat {X}^{\prime })>F(\hat {X})\), check the Metropolis acceptance criterion, i.e., if \(\exp (-\Delta \hat {F}/T_{t})>random(0,1)\), T t →0, t→∞, then \(X^{*}\leftarrow \hat {X}^{\prime }\).
Reinforce the pheromone trails on the nodes of \(\hat {X}\) and X ∗ and evaporate the pheromone trails on the left nodes:
where, ρ(0<ρ<1) is the evaporate rate, and g(x)(0<g(x)<+∞) is a function with that g(x)≥g(y) if F(x)<F(y). For example, g(x)=L/(|F(x)|+1) is an available function if L>0.
Now, we summarize the algorithm as follows. Step 1 Initialize all pheromone trails with the same pheromone level τ 0. Randomly generate a feasible solution X 0, and set optimal solution \(\hat {X}=X_{0}\). Set t←0. Step 2 Ant movement in probability following Equation 12. Generate a decision variable x i after m+1 steps. Step 3 Repeat Step 2 until decision vector X=(x 1,x 2,⋯,x n ) is generated. Build the neighbor solution X ′. If Δ F=F(X ′)−F(X)≤0, X←X ′; otherwise, if exp(−Δ F/t k )>r a n d o m(0,1) where t k is the current temperature and t k →0 when k→∞, then X←X ′. Step 4 Repeat Step 2 and Step 3 until all ants finish their walk, and generate M candidate solutions. Step 5 Calculate the system outputs by Equation 5. Then, calculate the objective function values for the M candidate solutions by Equation 11. Denote the best solution in this iteration by X t . Step 6 If \(F(X_{t})<F(\hat {X})\), then \(\hat {X}\leftarrow X_{t}\). Build the neighbor solution of \(\hat {X}\), which is denoted by \(\hat {X}^{\prime }\). If \(\Delta \hat {F}=F(\hat {X}^{\prime })-F(\hat {X})\leq 0\), then \(\hat {X}\leftarrow \hat {X}^{\prime }\); otherwise, if Metropolis acceptance criterion is satisfied, i.e., if \(\exp (-\Delta \hat {F}/T_{t})>random(0,1), T_{t}\rightarrow 0, t\rightarrow \infty \), then \(X^{*}\leftarrow \hat {X}^{\prime }\). Step 7 Update the pheromone trails according to Equation 14. Step 8 t←t+1; if t=T, terminate; otherwise, go to Step 2. Step 9 Report the optimal solution \(\hat {X}\).
Experiments
In this section, we use our two extraction methods to extract uncertain inference rules. And then use the uncertain systems to solve some classification problems. We applied our methods to the IRIS [26] classification problem and the Wisconsin Breast Cancer (WBC) [27] classification problem.
IRIS classification
IRIS data set is the typical date set in data classification. It contains 150 instances of 3 classes, which are Setosa, Versicolor, and Virginica. Each class has 50 instances. Each instance has 4 attributes which are sepal length (SL), sepal width (SW), petal length (PL), and petal width (PW). They are described by 3 uncertain sets: low (1), medium (2), and high (3). The membership functions are
where x is the input, β=0.618 and \(V_{q}=\frac {q-1}{2}\), q=1,2,3. Based on these 4 attributes, we try to infer which class does the instance belong to. We use 3 triangular uncertain sets η
p
=(a
p
,b
p
,c
p
)(p=1,2,3) to describe the possible classes (class 1: Setosa; class 2: Versicolor; class 3: Virginica). And the parameters  are listed in Table 1.
are listed in Table 1.
First, we normalize the data to [ 0,1] to simplify the computation. IRIS data set is our training set while it is also used for testing. Then, we set maximum number of rules n=10, number of ants M=10, evaporate rate ρ=0.3, and number of iterations T=300. Each algorithm runs ten times. The results are in Figures 1 and 2. Denote the extraction method with mutation by A and the method with SA by B. It can be seen that the method A converges fast at about 120th iteration. And method B converges a little slower at about 150th iteration.
Then, we can classify the IRIS data with the uncertain systems we introduced. We find the average accuracy rates of the two methods are 97.33% and 97.5%, respectively. Comparison with other methods are listed in Table 2.
List the rule bases we get with the highest accuracy rates (98.0% and 98.67%, respectively) in Tables 3 and 4. Note that although the maximum number of rules is 10, the final rule bases we obtain has only 7 rules.
Wisconsin Breast Cancer classification
Wisconsin Breast Cancer data set is a common medical date set. It contains 699 instances of 2 classes, which are sick and healthy. Two hundred forty-one instances are sick and 458 instances are healthy. Each instances has 9 attributes, which are clump thickness (CT), uniformity of cell size (UCS), uniformity of cell shape (UCCS), marginal adhesion (MA), single epithelial cell size (SPCS), bare nuclei (BN), bland chromatin (BC), normal nucleoli (NN), and mitoses (MT). They are described by 5 uncertain sets: very low (1), low (2), medium (3), high (4), and very high (5). The membership functions are
where x is the input, β=0.4247, and \(V_{q}=\frac {q-1}{2}\), q=1,2,3,4,5. Based on these attributes, we diagnose whether one instance is sick or not. We use 2 triangular uncertain sets η
p
=(a
p
,b
p
,c
p
)(p=1,2) to describe the possible classes (sick and healthy). And the parameters  are listed in Table 5.
are listed in Table 5.
First, we normalize the data to [ 0,1] to simplify the computation. The first 460 instances are used for training while the left 239 instances are used for testing. Then, we set maximum number of rules n=10, number of ants M=20, evaporate rate ρ=0.3, and number of iterations T=200. Each algorithm runs ten times. The results are in Figures 3 and 4. We still find that method A converges faster than method B. Method A stabilizes at about 50th iteration while method B stabilizes until about 80th iteration.
Then, we test the uncertain systems we get with the later 239 instances. We find the average accuracy rates of the two methods on the training set are 96.0% and 96.26%, respectively. Using the uncertain system with the highest accuracy rate of each method on the test set, we find the accuracy rates are 98.37% and 98.33%. Comparison with other methods are listed in Table 6.
The rule base with the highest accuracy rates (98.37% and 98.33%, respectively) on the test set are listed in Tables 7 and 8. Method A gives us a rule base of 9 rules, and method B provides a rule base of 6 rules.
We apply our two extraction methods to the classification problems of IRIS data set and WBC data set. Compare our results with other researchers’ work, we can find that both methods have higher accuracy rate than ACOA and MACO in two classification problems. And for IRIS data set, accuracy rates of method A and B are lower than HNFQ but higher than C4.5. For WBC data set, their accuracy rates are higher than C4.5 and FMM.
Conclusions
In this paper, we designed an uncertain system for data classification. And we proposed two extraction methods for uncertain inference rules by using ant colony optimization algorithm. Then, we applied our methods to IRIS classification problem and WBC classification problem. Our methods are shown to be superior in accuracy to some existing methods.
References
Kantardzic, M: Data Mining: Concepts, Models, Methods, and Algorithms. 2nd ed. Wiley, Hoboken (2011).
Quinlan, JR: Improved use of continuous attributes in C4.5. J. Artif. Intell. Res. 4(1), 77–90 (1996).
Parpinelli, RS, Lopes, HS, Freitas, AA: Data mining with an ant colony optimization algorithm. IEEE Trans. Evolut. Comput. 6(4), 321–332 (2002).
Casillas, J, Cordón, O, Herrera, F: Learning fuzzy rules using ant colony optimization algorithms. In: Proceedings of the 2nd International Workshop on Ant Algorithms: From Ant Colonies to Artificial Ants, pp. 13–21, Brussels (2000).
Zhu, Y: Ant colony optimization-based hybrid intelligent algorithms. World J. Modell. Simul. 2(5), 283–289 (2006).
Zhu, Y: An intelligent algorithm: MACO for continuous optimization models. J. Intell. Fuzzy Syst. 24, 31–36 (2013).
Lee, Z, Su, S, Chuang, C, Liu, K: Genetic algorithm with ant colony optimization (GA-ACO) for multiple sequence alignment. Appl. Soft Comput. 8(1), 55–78 (2008).
Shelokar, PS, Siarry, P, Jayaraman, VK, Kulkarni, BD: Particle swarm and ant colony algorithms hybridized for improved continuous optimization. Appl. Math. Comput. 188(1), 129–142 (2007).
Liu, B: Uncertainty Theory. 2nd ed. Springer, Berlin (2007).
Liu, B: Fuzzy process, hybrid process and uncertain process. J. Uncertain Syst. 2(1), 3–16 (2008).
Chen, X, Liu, B: Existence and uniqueness theorem for uncertain differential equations. Fuzzy Optimization Decis. Mak. 9(1), 69–81 (2010).
Liu, B: Some research problems in uncertainty theory. J. Uncertain Syst. 3(1), 3–10 (2009).
Liu, B: Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty. Springer, Berlin (2010).
Peng, J, Yao, K: A new option pricing model for stocks in uncertainty markets. Int. J. Oper. Res. 8(2), 18–26 (2011).
Zhu, Y: Uncertain optimal control with application to a portfolio selection model. Cybern. Syst. 41(7), 535–547 (2010).
Liu, B: Uncertain set theory and uncertain inference rule with application to uncertain control. J. Uncertain Syst. 4(2), 83–98 (2010).
Liu, B: Uncertain logic for modeling human language. J. Uncertain Syst. 5(1), 3–20 (2011).
Gao, X, Gao, Y, Ralescu, DA: On Liu’s inference rule for uncertain systems. Int. J. Uncertain. Fuzz. Knowledged-Based Syst. 18(1), 1–11 (2010).
Peng, Z, Chen, X: Uncertain systems are universal approximators. J. Uncertainty Anal. Appl. 2, Article, 13 (2014).
Gao, Y: Uncertain inference control for balancing inverted pendulum. Fuzzy Optimization Decis. Mak. 11(4), 481–492 (2012).
Liu, B: Membership functions and operational law of uncertain sets. Fuzzy Optimization Decis. Mak. 11(4), 387–410 (2012).
Zadeh, LA: Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 3(1), 28–44 (1973).
Mamdani, EH: Applications of fuzzy algorithms for control of a simple dynamic plant. Proc. Institution Electr. Eng. Control Sci. 121(12), 1585–1588 (1974).
Takagi, K, Sugeno, M: Fuzzy identification of system and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 15(1), 116–132 (1985).
Kirkpatrick, S, Gelatt, CD, Vecchi, MP: Optimization by simmulated annealing. Science. 220(4598), 671–680 (1983).
Iris dataset (1936). https://archive.ics.uci.edu/ml/datasets/Iris.
Wisconsin Breast Cancer Dataset (1992). https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Original).
de Souza, FJ, Vellasco, M, Pacheco MA: Hierarchical neuro-fuzzy quadtree models. Fuzzy Sets Syst. 130(2), 189–205 (2002).
Gabrys, B, Bargiela, A: General fuzzy min-max neural network for clustering and classification. IEEE Trans. Neural Networ. 11(3), 769–783 (2000).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (No.61273009).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, L., Sun, Y. & Zhu, Y. Extraction methods for uncertain inference rules by ant colony optimization. J. Uncertain. Anal. Appl. 3, 9 (2015). https://doi.org/10.1186/s40467-015-0033-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40467-015-0033-9
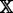 is ξ, then
is ξ, then 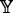 is η
is η
 is a constant a
is a constant a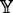 is η
is η
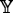 is η
1
is η
1
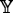 is η
2
is η
2
 is η
k
is η
k
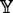 is determined by Eq. (
is determined by Eq. (


