- Research
- Open access
- Published:
Stochastic hierarchical multiobjective routing model in MPLS networks with two service classes: an experimental study on imprecision and uncertainty issues
Journal of Uncertainty Analysis and Applications volume 2, Article number: 3 (2014)
Abstract
The paper begins by reviewing a two-level hierarchical multicriteria routing model for Multiprotocol Label Switching networks with two service classes (Quality of Service and Best Effort services) and alternative routing, previously proposed by the authors. The features of the considered resolution heuristic are described. Some key issues raised by its complexity are discussed, as well as the major factors that constitute the sources of imprecision, inaccuracy, and uncertainty of the model and the way in which they are dealt with in the adopted resolution approach. Analytic and stochastic discrete-event simulation experiments are performed for different test networks, including experiments with a dynamic version of the routing method. This case study allows for the evaluation of the inaccuracies intrinsic to the analytic/numerical resolution procedures and of the uncertainty associated with the estimates of the mean of the stochastic traffic flows. An analysis focused on key robustness aspects of the model is also carried out.
AMS Subject Classification
Primary 90B50; secondary 90B18; 90B15
Introduction and motivation
In modern multiservice networks, multiple and heterogeneous Quality of Service (QoS) routing requirements have to be taken into account. Therefore, the routing models, which are designed to calculate and select sequences of network resources, have to satisfy certain QoS constraints while seeking to optimize route-related objectives. Formulating routing problems in these types of networks as multiple objective optimization problems is potentially advantageous, as the trade-offs among distinct performance metrics and other network cost function(s) can be pursued in a consistent manner when these multiple objective formulations are used.
Reviews on multicriteria routing models for communication networks are presented in [1] (in a broader context of multicriteria analysis applications) and in [2], which also discusses some key methodological issues and includes multiple research papers in this area. More recently, a complete conceptual framework in multiple criteria routing models in QoS/IP networks, considering a reference point-based approach is proposed in [3].
A meta-model for hierarchical multiobjective network-wide routing in Multiprotocol Label Switching (MPLS) networks is presented in [4]. In this approach, two classes of services, QoS and BE (Best Effort) type flows, and different types of traffic flows in each class are considered. A hierarchical optimization with two optimization levels, including fairness objectives, is considered: the first-priority objective functions (o.f.s) refer to the network-level objectives of QoS flows, namely the total expected revenue and the maximal value of the mean blocking of all types of QoS flows; the second-priority o.f.s refer to performance metrics for the different types of QoS services and the total expected revenue associated with the BE traffic flows.
In [5], a heuristic approach (HMOR-S2 PAS - H ierarchical M ultio bjective R outing considering 2 classes of S ervice with a P areto A rchive S trategy), devised to find ‘good’ solutions in the sense of multiobjective optimization (see [6]) to this hierarchical multiobjective routing optimization problem, is proposed and applied to two test networks used in a benchmarking case study, for various traffic matrices for each network. Remember that in the context of multiobjective optimization, the concept of optimal solution (usually unfeasible) is replaced by the concept of non-dominated (or Pareto optimal) solutions. A non-dominated solution may be defined as a feasible solution such that it is not possible to improve the value of an o.f. without worsening the value of at least one of the other o.f.s.
In [7], the same heuristic approach is applied to two other networks with more connectivity than the networks in [5]. The results of computational experiments using an analytical model and stochastic discrete-event simulation (with a static routing model where the network routing plan never changes) are presented, in order to evaluate the performance of the proposed heuristic in terms of the effect of the used route calculation and selection procedures.
Throughout the study of the routing model and the implementation of the resolution procedure, some factors of imprecision, inaccuracy (or inaccurate determination), and uncertainty (IIU, for short) of the routing model and their effects on the results of the routing method are taken into account by the authors. In this work, these factors are systematized and analyzed, having in mind their great importance in the context of the model. A broad discussion of modeling issues concerning IIU aspects in relation to multicriteria analysis is in [8].
In this work, a new set of stochastic simulation experiments with the heuristic approach proposed in [5] are presented in order to evaluate the inaccuracies intrinsic to the analytic/numerical resolution procedures. A state-dependent periodic-type dynamic routing model (where the network routing plan is updated as a function of the measured offered traffic in the network) is considered in these experiments. Different simulation parameters have a direct influence on the robustness of the results obtained with the dynamic model simulation. In particular, the effects in the model results of the uncertainty associated with the moving average estimates of the offered traffic in the network and the influence of the routing plan update time interval are analyzed, allowing for a robustness analysis focused on key robustness aspects of the model.
The paper is organized as follows. The two-level hierarchical multiobjective alternative routing model with two service classes and the features of the considered heuristic are briefly reviewed in the next section. Still in the same section, an analysis of the IIU factors associated with key instances of the model and its resolution and their potential effects on the heuristic results, is provided. The results obtained with this procedure, by using analytic and discrete-event simulation experiments for four test networks, are shown and analyzed in relation to the IIU factors, in the following section. These experiments provide some preliminary conclusions on the robustness of the method concerning some of the IIU factors. Conclusions are drawn in the last section. The paper ends with an Appendix with the specification of the notation used in the model and an Appendix with the formalization of the heuristic resolution approach.
Review of the multiobjective routing model and the heuristic resolution approach
The multiobjective routing model
The model addressed in this paper may be considered an application of the multiobjective modeling framework (or ‘meta-model’) for MPLS networks proposed in [4], as previously noted. It is a network-wide routing optimization approach (that is, the main o.f.s depend explicitly on all traffic flows in the network), in the form of a hierarchical multiobjective optimization model, which takes into account the nature and relations between the adopted o.f.s related to the different types of traffic flows associated with different services.
Two classes of services are considered: QoS, corresponding to services with certain guaranteed QoS levels (represented through the set ) and considered in the model as first-priority flows; BE (represented through the set ), regarded as second-priority flows, where the corresponding traffic flows are routed seeking the best possible quality of service to be obtained but not at the cost of the quality of service of the traffic flows belonging to . The traffic flows of each service type or may differ in important attributes, such as the required bandwidth.
The hierarchical multiobjective routing optimization model tackled here has two levels with several o.f.s in each level. At the first level, the first-priority o.f.s are considered: W Q (the total expected network revenue associated with QoS traffic flows) and BM m|Q (the worst average performance among QoS services, represented by the maximal average blocking probability among all QoS service types). These objectives are formulated at the network level for the QoS traffic and allow us to take into account the combined effect of all types of traffic flows in the network. The second level includes the second-priority o.f.s concerned with average performance metrics of the QoS traffic flows associated with the different types of QoS services (represented by Bm s|Q, the mean blocking probabilities for flows of type , and BM s|Q, the maximal blocking probability defined over all flows of type ) as well as W B , which represents the total expected network revenue associated with BE traffic flows. At both levels of optimization, min− max objectives constituting ‘fairness’ objectives are explicitly considered: at the first level, and at the second level, where denotes the routing plan (set of feasible node-to-node loopless paths) for all offered flows.
The considered two-level hierarchical optimization problem for two service classes P-M2-S2 (‘P roblem - M ultiobjective with 2 optimization hierarchical levels - with 2 S ervice classes’) is
subject to equations of the underlying traffic model.
The notation and basic formulae for the calculation of these o.f.s are in an Appendix at the end of the paper.
Note that in the formulation of P-M2-S2, W Q (together with BM m|Q) is a first-priority o.f., while W B is a second-level o.f. This assures that the routing of BE traffic, in a quasi-stationary situation, will not be made at the cost of the decrease in revenue or at the expense of an increase in the maximal blocking probability of QoS traffic flows. Nevertheless, it is important to note that while QoS and BE traffic flows are treated separately in terms of o.f.s so as to take into account their different priority in the routing optimization, the interactions among all traffic flows are fully represented in the model. In fact, the contributions of all the traffic flows which may use every link of the network are used to obtain the blocking probabilities B(f s ).
A full description of the traffic modeling stochastic approach used in the routing model can be seen in [4]. In the considered basic teletraffic model, the blocking probabilities B k s , for micro-flows of service type s in link l k , are calculated by , with representing the function (implicit in the teletraffic stochastic model) that expresses the marginal blocking probabilities, B k s , in terms of equivalent effective bandwidths d k s for all service types, reduced traffic loads ρ k s offered by flows of type s to l k and the link capacity C k . With this type of approximation (see [9]), the calculation of {B k s } can be made by efficient and robust numerical algorithms, which are essential in a network-wide routing optimization model of this type, for tractability reasons. In this situation, the classical Kaufman (or Roberts) algorithm ([10, 11]) can be used to calculate the functions for small values of C k . For larger values of C k , approximations based on the uniform asymptotic approximation (UAA) in [12] are used, having in mind its efficiency in these situations.
The decision variables represent the network routing plans, that is, the set of all the feasible routes (i.e., node-to-node loopless paths) for all traffic flows, with and R(f s )=(rp(f s )), p=1,⋯, M with M=2 in our model. That is, an alternative routing principle is used: for each flow f s the connection request attempts the first choice route r1(f s ); if it is blocked the second choice route r2(f s ) is tried. A request will be blocked only if r2(f s ) is also blocked.
The very high complexity of the routing problem P-M2-S2 stems from two major factors: all o.f.s are strongly interdependent (via the {B(f s )}), and all the o.f. parameters and (discrete) decision variables (network route plans) are also interdependent in terms of their effects.
Considering the form of P-M2-S2, one may conclude on the great intractability of this problem. Note that there are possible conflicts between the o.f.s in P-M2-S2: in many routing situations, the maximization of W Q leads to a deterioration on some B(f s ), , for certain traffic flows with low intensity and this tends to increase BM s|Q and Bm s|Q, and consequently, BM m|Q. This is a major factor that justifies the interest and potential advantage in using multiobjective approaches when dealing with this type of routing methods.
The heuristic resolution approach
The theoretical foundations of a specialized heuristic strategy for finding ‘good’ compromise solutions to the very complex bi-level hierarchical multiobjective alternative routing optimization problem, are presented in [13]. In [5], a heuristic procedure (HMOR-S2 PAS), devised to seek non-dominated solutions to this problem, is proposed and applied to test networks used in a benchmarking case study, for various traffic matrices. This heuristic resolution approach is briefly reviewed in this section.
This heuristic is based on the recurrent calculation of solutions to an auxiliary constrained bi-objective shortest path problem , formulated for every end-to-end flow f s ,
The two metrics mn to be minimized are the marginal implied costs and the marginal blocking probabilities for flows of service type s on link l k . These metrics are chosen because the metric blocking probability tends, at a network level, to minimize the maximal node-to-node blocking probabilities B(f s ), while the metric implied cost tends to maximize the total average revenue W T in a single class multiservice loss network ([14, 15]). The set of all feasible loopless paths for flow f s , , satisfies specific traffic engineering constraints for flows of type s. By using this approach, the efficiency of different candidate routes in the context of a multicriteria routing framework of this type can be compared by taking into account both the loss probabilities experienced along the candidate routes and the knock-on effects upon the other routes in the network, effects which are associated with the acceptance of a call on that given route. Such effects can be measured exactly through the marginal implied costs for QoS(BE) traffic, , associated with the acceptance of a connection (or ‘call’) of traffic f s of any service type on a link l k , that can be defined as the expected value of the traffic loss induced on all QoS(BE) traffic flows resulting from the capacity decrease in link l k (see [13]).
In the heuristic, the auxiliary constrained shortest path problem is solved by an algorithmic approach, MMRA-S2 (M odified M ultiobjective R outing A lgorithm for multiservice networks, considering 2 classes of S ervice) in [13], which aims at finding a ‘best’ compromise path from a set of non-dominated solutions, according to a system of preferences. The path computation and selection are fully automated; therefore, the system of preferences is embedded in the working of the algorithm. This is implemented by defining preference regions in the o.f. space obtained from aspiration and reservation levels (preference thresholds) defined for the two o.f.s ([14, 15]), as will be explained later.
The candidate solutions (r1(f s ), r2(f s )) for each f s are generated using MMRA-S2. They are selected (or rejected) according to specific criteria, to be ‘tuned’ throughout the execution of the heuristic. A maximal number of arcs D s per route for each service type s is previously defined and a feasible route set D(f s ) is obtained for each f s .
Notice that the successive application of MMRA-S2 to every traffic flow does not lead to an effective resolution approach to the network routing problem P-M2-S2, as anticipated by the theoretical analysis of the model and confirmed by experimentation. This results from an instability phenomenon arising in such path selection procedure, expressed by the fact that the route sets often tend to oscillate between specific solutions some of which may lead to poor global network performance under the prescribed metrics. This instability phenomenon is associated with the complexity and interdependencies in the addressed problem P-M2-S2, namely the interdependencies between and {B k s } and between these two sets and the current network route set .
Therefore, it is necessary to search for the subset of the path set, the elements of which should be possibly changed in the next route improvement cycle, which constitutes another core idea of the heuristic approach. A criterion for choosing candidate paths for possible routing improvement by increasing order of a function ξ(f s ) of the current (r1(f s ), r2(f s )) is proposed in [16]. Preference (concerning the potential value in changing the second choice route when seeking to improve W Q or W B ) is given to the flows for which the route r1(f s ) has a low implied cost and the route r2(f s ) has a high implied cost, or to the flows which currently have worse end-to-end blocking probability.
In a basic version of the heuristic, HMOR-S2, each new solution is obtained by processing the current best solution. A basic searching strategy is to seek for routing solutions R(s) for each service , in order to achieve a better performance in terms of W B (if ) or Bm s|Q and BM s|Q (if ), while respecting the hierarchy of o.f.s. This also means that network resources are left available for traffic flows of other services so that the solutions selected at each step of the procedure may improve the first-priority o.f.s W Q and BM m|Q. The heuristic is designed in order to seek, firstly for each QoS service and, secondly, for each BE service, solutions which dominate the current one, in terms of Bm s|Q and BM s|Q for QoS services and in terms of W B for BE services. These solutions are accepted only if they do not lead to the worsening of any of the network functions W Q and BM m|Q.
Due to these strict limitations imposed on the acceptance of a new solution, there is the realization that some potentially interesting solutions to the routing problem are not further pursued. Therefore, throughout the execution of the basic heuristic some possibly interesting solutions are stored and later checked, seeking to find a ‘best’ possible solution to the problem in hand [5].
The steps of this heuristic resolution approach are explicitly written out in an Appendix at the end of the paper.
Dealing with imprecision, inaccuracy, and uncertainty in the model
The development of the routing model and the implementation and application of the resolution procedure put in evidence the importance of IIU factors of the routing model and their impacts on the results of the routing method. In this subsection, an analysis and a systematization of these factors in the context of the model are presented. In Table 1, a summary of the sources of IIU is presented. Also, the way these aspects are dealt with in our resolution approach are discussed (and summarized in Table 1) or a brief explanation as to why these aspects do not have a significant impact on the final results is provided.
Imprecision factors
The imprecision factors stem mainly from the approximations inherent to the analytic traffic model (underlying the optimization model), namely a superposition of independent Poisson flows and independent occupations of the links. A general description of the stochastic traffic models associated with this issue can be seen in ([17], Chapter 6). An exact model which might be in principle applied to these networks is in [18], which is based on the consideration of MMPPs (Markov Modulated Poisson Processes) for representing the superposition of the overflows (resulting from the alternative routing) from independent Poisson processes. The type of considered simplification leads inevitably to intrinsic imprecisions in the values of the traffic parameters which are reflected in the calculation of the o.f. values. Still, if a more accurate and realistic representation of the traffic flows is used, better estimates of the blocking probabilities will be achieved. Nonetheless, the approximations in our model can be considered appropriate and, above all, absolutely necessary in this context, for practical reasons. In fact, if more exact stochastic models are used to represent the traffic flows and to calculate the blocking probabilities in overflow conditions such as the one in [18], the computational burden will be too heavy since the analytical model has to be numerically solved many times during the execution of the heuristic and the routing method will become intractable in terms of memory and processing time requirements.
Some imprecision also arises from the numerical errors, associated with the resolution of the system of equations of the traffic model which propagate throughout the resolution procedure, as the resolution of the traffic model has to be performed many times (in the calculations of marginal implied costs and blocking probabilities of all the flows). To minimize the latter imprecision effects, some ‘robust’ and well-tested classical numerical algorithms (namely the Kaufman/Roberts algorithm ([10, 11]) and fixed-point iterators ([19])) are used to estimate the blocking probabilities in the system. Moreover, these two types of errors do not compromise the inequality relations between the o.f. values, as the aim of the routing optimization procedure is just the comparison of routing solutions in terms of the values of the o.f.s. That is, the focus of the tackled multiobjective optimization model is on the relative value of the results of the traffic model rather than on the absolute accuracy of such values. Also, small differences between o.f. values can be disregarded when comparing solutions.
Further imprecision effects stem from an instability phenomenon which may potentially arise in the path selection procedure. In fact, the route sets , if obtained by successive application of MMRA-S2 to every traffic flow, often tend to oscillate between certain solutions some of which may lead to poor global network performance under the prescribed metrics, thus leading to uncertainty in the results. The experimentations confirm that the successive application of MMRA-S2 to every traffic flow does not lead to an effective resolution approach to the network routing problem P-M2-S2. For dealing with this issue in a successful manner, detailed analysis and extensive experimentation with the heuristic have led to the proposal of a criterion for choosing candidate paths for possible routing improvement by increasing order of a function ξ(f s ) of the current routes of a flow f s , giving preference (concerning the potential value in changing the routes when seeking to improve the QoS(BE) traffic revenue) to the flows for which the first route has a low implied cost and the second route has a high implied cost, or to the flows which currently have worse end-to-end blocking probability.
Inaccuracy factors
The inaccuracies are a consequence of the high complexity of the routing problem P-M2-S2 stemming from the combinatorial nature of the global routing multiobjective optimization problem and are related to two major factors specific to the described model: all o.f.s are strongly interdependent (via the B(f s )) and all the o.f. parameters and (discrete) decision variables (network route plans) are also interdependent in terms of their effects in the problem solutions. These interdependencies result from the fact that all the specified o.f.s depend on all traffic flow patterns in the global network, which may change significantly with any alteration in any route choice for any given node-to-node flow. This mechanism generates potential instability in the global routing solutions, as analyzed in a similar yet simpler model in [15]. Note that all these interdependencies are defined explicitly or implicitly through the underlying traffic model.
Also, note that even in the simplest degenerated case (single service with single-criterion optimization and no alternative routing), the problem is NP-complete in the strong sense, as proved in [20]. This high complexity leads to inaccurate results, because the solutions of the routing problem are inherently approximate. In fact, when heuristic solution techniques are employed, the resolution method does not calculate all the non-dominated solutions and even for those selected solutions which are computed there is no certainty that they are not potentially dominated by other solutions. Concerning the possibility of not detecting the condition of certain weakly dominated solutionsa this may be explained by small variations in the values of some o.f.s for certain solution(s) close to the current one (for example, by changing a single route for a given flow), solution(s) which, in some cases, may not be detected by the heuristic. It must be remarked that this occurrence is rare but in principle may arise. The mechanisms of the heuristic resolution in its present version (HMOR-S2 PAS), as described in the previous sub-section, are devised to deal with this issue in order to minimize the impact of these inaccuracies in the quality of the obtained compromise solutions.
Uncertainty factors
As for the uncertainty issues, they are raised mainly by the stochastic nature of the offered traffic and the related estimation procedures performed throughout the stochastic simulation experiments with the proposed heuristic. In the classification framework discussed in [21], this type of uncertainty may be considered as an ‘external uncertainty’, as it relates to a form of uncertainty that results from environmental conditions (the stochastic traffic load conditions in the network) of the model that cannot be controlled by the decision maker.
A particular form of ‘internal uncertainty’ (in the sense discussed in [21]) may be identified in the context of this model. This type of ‘uncertainty’ has to do with the identification and representation of the decision maker preferences. Noting that the model is supposed to be applied in an automated manner and following our previous experience in this area [5], we have developed a solution selection procedure based on the definition of dynamic preference thresholds in the o.f. space, combined with the use of reference points, inspired by the methodology described in [22]. This corresponds to imbedding the preferences of a ‘virtual decision maker’ in the form of a specific, problem-oriented, procedure of selection of non-dominated solutions. The effectiveness of such solutions is tested a posteriori using a simulation test-bed, applied in various typical application scenarios. For further details on the solution selection procedure, see [5].
In order to evaluate the effect of these uncertainty factors in the model results, an experimental study consisting of stochastic simulation experiments is performed. In the discrete event stochastic simulation experiments performed with a static routing model, a measurement of the degree of uncertainty of the o.f. values can be obtained by applying a classical statistical procedure (batch means with independent replications). As for the state-dependent periodic-type dynamic routing model, the traffic flow means are periodically updated via a statistical estimate, namely a first-order moving average, based on real-time measurements, dependent on a parameter b (fixed a priori), as explained in the ‘Simulation experiments’ section, which is another source of statistical uncertainty. This requires a sensitivity/robustness analysis, for the evaluation of the influence of this parameter and of the routing plan update time interval on the final global routing solution.
Note that the problem that is being considered here is not a ‘classical’ problem of decision under uncertainty as discussed in depth in [21]. A classical approach to that type of problem is the use of expected utility theory to planning under uncertainty, while our model may be considered as a specific type of multicriteria optimization model with stochastic variables. In the model, the o.f.s are means or probabilities defined in a classical probability theory framework.
Experimental study
In this section, the analytical and simulation results obtained with the HMOR-S2 PAS heuristic in four different networks are presented. The analytical results are obtained by a single run of the heuristic and the results for the QoS flows revenue W Q may be compared with theoretical bounds for the same function. As for the simulation results, they allow for a more realistic assessment of the results of the heuristic having in mind the combined effects of the analyzed IIU factors.
This set of experiments represents a set of scenarios [21], in the sense that each experiment has its specific features and allows for the analysis of relevant working conditions that can be encountered in actual networks. Notice however that the use of scenarios in this context is not for the evaluation and development of alternative solutions (a technique often used in multiattribute models, as extensively analyzed in [21]), but rather to explore the different possibilities that may arise in the routing context, having in mind to test the robustness and effectiveness (in terms of performance) of the solution selection procedure. This is achieved by considering scenarios of implementation of static and dynamic versions of the model and the consideration of three situations of load/overload conditions.
Two types of simulation are considered, one corresponding to a static routing model where the routing plan calculated by the heuristic is never changed regardless of the random variations in offered traffic throughout the simulation, for a given matrix of mean traffic offered in statistical equilibrium. The other corresponds to a periodic type state-dependent dynamic routing model, where the routing plans are updated periodically as a function of real-time traffic measurements, by using the heuristic HMOR-S2 repeatedly. Dynamic routing in a telecommunications network is a well-known routing principle where the most recent information on the network conditions is taken into account in order to find appropriate paths for the connection requests in the network. This is especially important when there are significant fluctuations of the offered traffic in various parts of the network, in particular as a result of overload or network failures. A comprehensive text on dynamic routing in telecommunication networks can be seen in [23].
For each of these two types of simulation, we consider three relevant network scenarios regarding the random fluctuations of traffic that are typical of stochastic traffic models: a deterministic scenario; a scenario where calls arrive according to a Poisson process, service times follow an exponential distribution and the network is critically loaded; a scenario where traffic flows have a higher ‘variability.’ The analysis of the results of each of these scenarios in each of the types of simulation gives an insight on the possible effects of inaccuracies intrinsic to the model and to the analytic/numerical resolution method on the results of the heuristic resolution procedure and also enables the verification of the effectiveness of the selected solutions, hence implementing a specific form of robustness analysis.
Application of the model to a network case study
The benchmarking case study considered here is based on the one in [24], where a model for traffic routing and admission control in multiservice, multipriority networks supporting traffic with different QoS requirements, is proposed. Deterministic models are used in the calculation of paths, in particular mathematical programming models based on Multicommodity Flows (MCFs). These models can be adapted to a stochastic traffic environment by using a simple technique: the requested values of the flow bandwidths in the MCF model are compensated with a factor α≥0.0, so as to model the effect of the random fluctuations of the traffic that are typical of stochastic traffic models. In the application example in [24], three values of α are proposed: α=0.0 corresponds to the deterministic approach; α=0.5 is the compensation factor when calls arrive according to a Poisson process, service times follow an exponential distribution and the network is critically loaded; and α=1.0 for traffic flows with higher ‘variability.’
The o.f.s of this problem, to be maximized, are the revenues W Q and W B , associated with QoS and BE flows. A bi-criteria lexicographic optimization formulation including admission control for BE traffic is considered, concerning the revenues W Q and W B , so that the improvements in W B are to be found under the constraint that the optimal value of W Q is maintained.
In the deterministic flow-based model in [24], a base matrix T= [ T i j ] with offered bandwidth values from node i to node j [Mbps] is given. A multiplier m s ∈ [ 0.0;1.0] with is applied to these matrix values to obtain the offered bandwidth of each flow f s with service type s. The transformation of this type of matrix into a matrix of offered traffic A(f s ), used in our stochastic traffic model, is achieved by if and both T(f s )=m s T i j and A(f s ) are high. Otherwise, where u0=16 kbps is a basic unit of transmission [bit/s].
Network 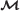
The routing model in [24] and the one considered here can be applied to the test network depicted in Figure 1. It has nodes, with ten pairs of nodes linked by a direct arc and a total of unidirectional arcs, giving an average node degree for this network of . The bandwidth of each arc [Mbps] is shown in Figure 1. The number of channels C k is , with basic unit capacity u0. A total of service types with the features displayed in Table 2 are considered. The values of the required effective bandwidths [channels] are also in the table (where is the required bandwidth in kbps). The expected revenue for a call of type s is assumed to be . The average duration of a type s call is h s and D s represents the maximum number of arcs for a route of a type s call. The application example in [24] provides upper bounds for the optimal value of the QoS traffic revenue W Q in our model.
Test network. This test network (with the indication of the bandwidth of each arc , in Mbps) is in [24].
Network 
In another set of tests, the considered routing model is applied to another test network (depicted in Figure 2), so as to further grasp the potential of the proposed heuristic strategy. Network has nodes, with 12 pairs of nodes linked by a direct arc and a total of unidirectional arcs, giving an average node degree for this network of . The bandwidth of each arc (Mbps) is shown in Figure 2. This test network is based on the network, in [25], dimensioned for extremely low blocking probabilities. This network has a topology similar to the one in Figure 3, with a capacity of Mbps for each arc, which is equivalent to a capacity of channels. The changes in the network by eliminating a few links allow for the achievement of slightly higher blocking probabilities. The traffic matrix remains the same as in the original reference ([25]). The information on the network and on the traffic matrix is used as an input to the routing model considered here. A comparison of the traffic that is offered to each of the networks and for each α shows that the offered load is lower in  .
.
Test network. This test network (with the indication of the bandwidth of each arc , in Mbps) is in [25].
Network topology for test networks  and
and  . For information on this network topology, see [25].
. For information on this network topology, see [25].
The service features are the same as for the tests with network and they are displayed in Table 2. Notice that the network diameter of network (equal to 4) is higher than the network diameter of network (equal to 3), which will influence the value of D s . These networks have similar density since their average node degree δ is practically the same.
In [25], no results concerning any of the o.f.s considered here are provided, as their multiobjective routing model is radically different from the one considered here. The only results that can be extracted from the proposed model in [25] are approximate ideal values for the QoS flows revenue, .
Networks 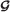 and
and 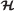
For the final set of tests, the considered routing model is applied to test networks and, for which the topology is depicted in Figure 3. They have nodes, with 16 pairs of nodes linked by a direct arc and a total of unidirectional arcs, giving an average node degree for these networks of . These networks have greater density than networks and. The bandwidth of each arc (Mbps) for each of the networks (obtained by employing a very simple network dimensioning algorithm) is shown in Tables 3 and 4.


The test networks and can be obtained after a redimensioning of the original network given in [25]. The offered traffic matrix remains the same as in [25]. A value β s for the mean blocking probabilities for flows of type s, B m s , is established, with a possible variation of Δ B .
Considering a routing method for network using only the shortest path direct routing (typical of Internet conventional routing algorithms), the mean blocking probabilities B m s are calculated. Once these values are known, they are compared with the established values at the beginning of the algorithm. If for service s, B m s >β s then the links in paths for flows of service s have their capacity increased. On the contrary, if for service s, B m s <Δ B β s , then the links in paths for flows of service s have their capacity decreased. The algorithm proceeds iteratively until it converges (which means that ). Sometimes, the algorithm oscillates between two different solutions, preventing it from converging. Therefore, a maximum number of runs has to be established, so as to avoid this situation.
This very simple network dimensioning algorithm can be used for the dimensioning of test networks and, for β s =0.1 and β s =0.12, respectively, with Δ B =0.9, that is, a situation of very high blocking is considered, associated with traffic overload for all services, for α=0.0. The purpose is to carry out comparisons of the performance of the considered static and dynamic routing methods in overload conditions (α=0.0) and in low and very low blocking conditions for the QoS traffic for α=0.5 and α=1.0. The original network is not used in this study because it is dimensioned for extremely low blocking probabilities.
The traffic matrix T= [ T i j ] with offered total bandwidth values from node i to node j [Mbps] remains the same as in the original reference ([25]). As with the tests performed for network, the modified version of the network and the traffic matrix are the only data taken from [25]. This information is used as an input to the routing model considered here.
These two networks and have more connectivity than networks and. The service features are the same as for the tests with the other networks. The ideal optimal values for the QoS flows revenue, , are calculated from the data in [25] and can be used for comparison purposes, as done for network.
Analytical experiments
In the analytical study, the HMOR-S2 heuristic (basic version of the heuristic without storage of non-dominated solutions) is run once, followed by a run of the HMOR-S2 PAS heuristic.
The initial solution is typical of Internet routing conventional algorithms: only one path for each flow (i.e., without an alternative path) is considered; the initial solution is the same for all the services and the paths are symmetrical; the path for every flow f s is the shortest one (that is, the one with minimum number of arcs); if there is more than one shortest path, the one with maximal bottleneck bandwidth (i.e., the minimal capacity of its arcs) is chosen; if there is more than one shortest path with equal bottleneck bandwidth, the choice is arbitrary.
The routing plan obtained at the end of the HMOR-S2 run for each specific α is the initial solution of HMOR-S2 PAS. This heuristic is run only once. For the archived routing plans obtained at the end of this single run, values for all the o.f.s are computed and the ‘best’ possible solution in the best possible preference region is chosen to be the final solution of the algorithm, using a reference point-based procedure as the solution selection mechanism, as in [5].
For the experiments with HMOR-S2 PAS, an archive of size 5 is considered, chosen empirically after extensive experimentation. Here, the practical conclusion is that an increase in the archive size will not necessarily lead to better final results because at the end of the heuristic run (when the final solution is chosen from those in the archive) the top 5 solutions tend to be the same regardless of the archive size (≥5).
Simulation experiments
Simulation experiments, with static and dynamic routing methods using the solutions provided by the heuristic, can also be carried out. The purpose of this simulation study is the validation of the routing model results and the evaluation of the errors intrinsic to the analytical model which provides the estimates for the o.f.s.
In a first set of experiments, the discrete-event stochastic simulation is applied to a static routing model, where the routing plan is the final solution obtained after the HMOR-S2 PAS run. This routing plan does not change throughout the simulation regardless of the random variations of traffic offered to the network. After an initialization phase that lasts for a time tw a r m−u p (that should be long enough to guarantee that the system state at the end of the initialization phase is representative of the steady-state behavior of the system), information on the number of offered calls and carried calls in the network for each flow , is gathered, until the end of the simulation. With this information, and subsequently, the values of the upper- and lower-level o.f.s related to blocking probabilities can be estimated. The calculation of the expected revenues is based on the number of carried calls in the network.
In the periodic and state-dependent dynamic version of the routing method considered here, the network state is assessed periodically and the gathered information on that state is used to periodically choose the most appropriate paths in the network, according to the HMOR-S2 routing algorithm. In the time interval [ n τ;(n+1)τ[, the estimate of the average traffic offered to the network by the flow f s is given by , obtained from a first order moving average iteration of the type
where is an estimator of the average value of the traffic offered by f s to the network in the previous interval [ (n−1)τ;n τ[. The value of b∈]0.0;1.0[ is a compromise between the need to obtain a quick response of the estimator to rapid fluctuations in and the stability of the long-run variations and should be settled by extensive experimentation with the simulation model. The parameter τ is both the update period of the estimates of the offered traffic and the update period of the network routing plans. Note that the process of path choice should take a short time, when compared to τ.
The routing method seeks to obtain new routing plans adapted to the changing network working conditions resulting from the random fluctuations of traffic intensities. Taking into account the features and great complexity of the routing model, the choice of the ‘start-up’ routing solution of the dynamic method is of great importance concerning its performance. The start-up solution is the final solution obtained after the HMOR-S2 PAS is run. The availability of a good estimate of the initial nominal traffic matrix is a necessary requirement of this dynamic routing method. Having in mind the periodically updated characteristics of the offered traffic, the ‘best’ possible set of paths is chosen so as to improve the multidimensional network performance, as specified by the multiobjective routing model.
A first phase of simulation, the initialization phase, lasts for a time twarm-up=t0+t1. In a first stage that lasts t0, only periodical updates of the estimate of the offered traffic are performed, with period τ. After that time t0, the offered traffic estimates are assumed to be representative of a steady-state behavior. Afterwards, during a time t1, the estimate of the offered traffic is still performed with a period τ, along with periodical updates of the routing plan, with the same period τ.
After the warm-up time, both updates are still performed with the indicated period and based on information on the number of offered calls and effectively carried calls in the network for each flow gathered from real-time measurements, until the end of the simulation. Using this information, a calculation of B(f s ) estimates () can be made, as well as a calculation of the values of all the upper- and lower-level o.f.s related to blocking probabilities. As for the revenues, the knowledge of the effectively carried calls in the network allows for the calculation of the carried traffic estimates, hence the calculation of revenues follows straightforwardly.
Comments on the experimental results
In Tables 5, 6, 7, and 8, the analytical values of each o.f. are displayed, together with the simulation results (average value ± half length of the 95% confidence interval) for these functions. The revenue values have two decimal places and the blocking probability values have three significant figures.
In the simulation experiments, a total of six seed files for random number generation are used, so the number of the performed independent runs is R=6, for each α. To illustrate the way in which the 95% confidence interval is calculated, take the example of the QoS revenue, W Q . An estimate of its average value is and an estimate of its variance is where WQ|i is the QoS revenue value for the i-th run, i=1,⋯, R. Considering a two-sided Student t-distribution, the confidence interval for W Q is where the critical value of t is t0.025;R−1=t0.025;5=2.57 (see [26], Table A.4).
For the static model simulation, different values for the warm-up time can be tried, and the results displayed in the tables correspond to those obtained with twarm-up=8 h for a total simulation time of 48 h. For the dynamic model simulation (which represents an innovative aspect of the extensive study conducted with this routing model in these networks), different values for the times t0 and t1, for τ and for b can be tried, and the results displayed in the tables correspond to those obtained with t0=t1=4 h; different values of τ; b=0.3; total simulation time of 48 h.
Analytical results
The resolution heuristic manages to start off with an initial solution with poor values for the o.f.s and still finish with a solution with significantly better values. The values for all the o.f.s for all values of α are improved through the heuristic. The QoS revenue of the final solutions is only slightly worse than that of the ideal optimal solutions, as expected. Therefore, we can consider that the resolution heuristic has managed to find an adequate ‘good’ compromise routing solution to the routing problem P-M2-S2. In fact, these experimental results for three traffic matrices for each network show that the expected QoS revenue obtained with our heuristic is never less than 99.47% of that upper bound while a substantial improvement on the other o.f.s can be obtained with respect to the initial solution, using only shortest path first choice routing, typical of Internet routing conventional algorithms.
Simulation results
The analytical results and the corresponding static routing model simulation results are of similar magnitude, but the analytical results tend to be better, as expected. In particular, considering the results obtained for network, the analytical results for the QoS flows revenue W Q are clearly better than the corresponding static routing model simulation results, for all the values of α. Generally speaking, for this network, the analytical results are not inside the 95% confidence interval of the static routing model simulation results and only for α=0.0 do we get a result where a first-level o.f. (BM m|Q) analytical value is in the corresponding confidence interval. Remember that the simulation results for the routing model are average values of performance in a great number of routing update intervals, while the analytical results are obtained in ideal steady-state traffic conditions and use approximate teletraffic sub-models.
For the other networks, the analytical and the simulation results for W Q are much closer and the analytical result for that o.f. is inside the 95% confidence interval for α=0.0 and α=0.5. For α=1.0, the analytical value of W Q is actually worse than the corresponding simulation result. In this situation of lower traffic load in networks , there are many instances throughout the executed simulations where the blocking estimate for certain services is 0, meaning that all the offered calls of those services are actually carried. This is the reason why so high values of the estimate of the QoS traffic revenue are obtained, surpassing the analytical values. Note that these are situations where the occurrence of blocking is a rare event. It is well known in statistics that in these cases, the uncertainty in the estimates is very high, as reflected in the very high relative half length of the calculated 95% confidence intervals of the blocking probabilities.
The differences between the analytical and the simulation results for the static routing model are mainly due to the imprecision effects intrinsic to the analytic/numerical solution, in particular those associated with the simplifications of the traffic model, and the associated error propagation. The analytical model is a simplification which tends to underestimate the blocking probabilities in the network (and therefore to overestimate the revenues), because the overflow traffic is treated as Poisson traffic. This error propagates throughout the complex and lengthy numerical calculations associated with the solution of the traffic model, involving the solution of large systems of implicit non-linear equations. Further simplifications assumed in the stochastic model for the traffic in the links are a superposition of independent Poisson flows and an independent occupation of the links. Although we envisage that a more precise and realistic representation of the traffic flows allows for better estimates of the blocking probabilities, the approximations in our model can be deemed appropriate and actually unavoidable in this context. This results from a compromise between the precision of the representation of the traffic flows and the computational burden of the numerical resolutions throughout the execution of the heuristic algorithm. For this reason, some robust and well-tested classical numerical algorithms (the Kaufman/Roberts algorithm and fixed-point iterators) are used to estimate the blocking probabilities of this system. It is important to note that as previously mentioned the type of error introduced by this approach does not compromise the inequality relations between the o.f. values. In fact, the focus of the optimization model is on the relative value of the results of the traffic model rather than on the absolute accuracy of such values, as explained in the sub-section on Dealing with IIU in the model.
The stochastic nature of the traffic offered to the network leads to some uncertainty in the results. In particular, for the state-dependent periodic-type dynamic routing model, the traffic flow means are periodically updated (with period τ) via a statistical estimate (first-order moving average) based on real-time measurements, dependent on a parameter b. The influence of these parameters on the final global routing solution can be analyzed.
In a first set of experiments, the update period τ is fixed and different values are tested for b. This parameter has to be set in order to reflect a compromise between the stability of the estimate and the quick response to variations in the partial estimate of the average value of the traffic offered by a flow to the network in the previous interval, . The best results for the first-level o.f.s can be obtained with b=0.3 (those are the values displayed in Tables 5, 6, 7, and 8). For b=0.4, the results are only slightly worse. However, for smaller values and for higher values of b, the results for W Q and BM m|Q are worse than those displayed in the tables. An increase(decrease) in b means that the estimate of the average traffic offered to the network by a flow, , gives more(less) importance to information on the previous interval and less(more) importance to the previous estimates of traffic obtained throughout the duration of the experiment. These results show that a balance between these two aspects is clearly desirable and no excessive weight should be attributed to either of them. However, as the best results are obtained with b<0.5, it appears that the stability of the estimate is slightly more important than a rapid response to variations in the offered traffic. Note that these results are in accordance with the traffic engineering recommendations in [27]. Notice that the possibility of network changes or sudden strong alterations in traffic patterns are not being considered in this study. This type of events would have required the traffic estimate to be able to respond better to very rapid variations in the offered traffic, so a value of b>0.5 would have been expected to be more appropriate in that situation. Probably, that would have been the case if the network traffic in the simulation model was not modeled as Poisson traffic but rather as self-similar traffic, with its typical bursts of traffic (see for instance [28]), a situation out of the scope of the present study. In a second set of experiments, the parameter b is kept at 0.3 and different values are tested for the update period τ. The best results for the first-level o.f.s are those obtained with τ=10, 20, 30 m (these values are displayed in Tables 5, 6, 7, and 8). Only for these parameter values is the dynamic routing model capable of attaining the performance values corresponding to the analytic upper bounds for the static solution. For other parameter values, the experimental results are not so good.
A final remark on the confidence intervals for each o.f.: their length is of the same order for both the static and the dynamic routing model.
The results for network, which is not dimensioned for low blocking probabilities, have shown that for a smaller value of τ (5 m), the results for W Q and BM m|Q are slightly worse than those displayed in Table 5. However, for a higher value of τ (30 m), the results are also worse (see Table 5). Therefore, in situations of high blocking probability, there is no need to update the traffic estimate too often (with update periods of the order of only a few minutes), but a very long update period is also undesirable. Notice that a value of b=0.3 means that the update information focuses more on the medium/long term rather than on the short term, as the estimate of the average traffic offered to the network by a flow incorporates more information on the estimates of traffic that have been obtained throughout the duration of the experiment, rather than on the previous interval. In very long intervals, slight changes in the offered traffic pattern are more likely to occur and these tend to be disregarded, if the update periods are very long (30 min or more) because of the lower importance given to the information on the specific previous interval, in the traffic estimate.
For higher values of α (corresponding to lower load), we realize that the simulation results for each of the networks are the same regardless of the value of τ. As mentioned earlier, these networks, for α=0.5 and α=1.0, are dimensioned for low blocking probabilities, and the blocking estimates are close to 0 in many cases, as all the offered calls tend to be carried. In this case, the total expected network revenues associated with QoS and BE traffic flows tend to have maximum values regardless of the value of τ.
In global terms and as expected, the results obtained with the dynamic routing model are better (or approximately the same in the worst case) than those obtained with the static routing model. This is especially noticeable for α=0.0 for all the networks, which is the situation of higher load. This shows that in situations of higher load, the dynamic model is well calibrated for these networks, in terms of the choice of the initial routing solutions to be used by the heuristic and the choice of the routing updating period. In the dynamic routing model, the routing plan is adjusted throughout the simulation run, in accordance with the traffic random fluctuations around the average values corresponding to the nominal traffic matrix defined in steady-state conditions.
The o.f. values are intrinsically imprecise, due to the simplifications and approximations assumed in the stochastic model for the traffic in the links, and to the numerical errors associated with the resolution of the system of equations of the traffic model which propagate throughout the resolution procedure. Still, the representation of the traffic flows as independent Poisson processes and the independence in the occupations of the links may be considered a good compromise between the exactness of the traffic model and the computational burden for solving the analytical model.
Other imprecision effects are due to an instability phenomenon which may potentially arise in the path selection procedure, when all the network routes are liable to change. To avoid oscillations between certain solutions that can possibly lead to a poor global network performance, the core algorithm that seeks new routing solutions (MMRA-S2) is applied only to specific traffic flows that are carefully chosen (according to the value of ξ(f s ), as mentioned earlier), so as to try and improve the o.f. values.
The inaccuracy in the o.f. values may be considered inevitable, due to the very great combinatorial complexity of the optimization model including strong interdependencies among key mathematical entities of the model. The heuristic resolution has different mechanisms, throughout the improvement cycles of the o.f.s, which try to deal with these complex interdependencies, in order to minimize the impact of these inaccuracies in the quality of the obtained compromise solutions.
Conclusions
In this paper, a stochastic two-level hierarchical multiobjective routing model for MPLS networks with two service classes and alternative routing was reviewed and analyzed concerning sources of imprecision, inaccuracy (or inaccurate determination), and uncertainty (IIU). Key issues raised by its high complexity were discussed in a systematic manner, as well as the major factors that constitute the sources of IIU of the model. The mechanisms used by the developed resolution heuristic approach to deal with these issues were also described.
The most important innovative aspect of this paper was the presentation of analytical and stochastic simulation experiments (both for static and dynamic versions of the routing model), enabling the evaluation of inaccuracies intrinsic to the model and to the analytic/numerical resolution method, as well as the evaluation of a particular form of ‘internal uncertainty’ associated with the necessity of representing a system of preferences (of a ‘virtual decision maker’) in a fully automated application. The possible effects of these inaccuracies on the results of the heuristic resolution procedure were discussed as well as the forms of minimizing their impacts on the heuristic effectiveness. Furthermore, the experimental study, using discrete-event stochastic simulation, enabled the validation of the routing model results and the evaluation of effects in the model results of the uncertainty associated with the offered traffic estimates, in a dynamic version of the routing method.
The analysis of these types of IIU factors, their effects on the results of the resolution approach of the routing optimization model, and the described general type of procedures for dealing with these issues are in our opinion relevant to other routing models with similar features. That is, we think that dealing with these issues in a proper manner is an important task in the context of multiobjective routing models, based on network-wide optimization approaches (where the combined effect and interactions among the traffic flows have to be explicitly represented) and using a stochastic representation of the traffic flows. Having in mind the high complexity and heavy numerical costs of the addressed model, probably several of the methods and techniques used for dealing with these IIU issues, may be adapted to various network routing models of similar nature. This is naturally an important task that justifies future works on IIU issues (and the ways to deal with these issues) focused on specific types of stochastic network-wide routing optimization models.
Endnote
a A weakly dominated solution is a feasible solution such that there is at least another feasible solution with better values for some of the o.f.s and equal values for the other o.f.s.
Appendix
Notation used in the model
The notations used in the model are shown in Table 9.
Formalization of the heuristic resolution approach
The formalization of the heuristic approach (HMOR-S2 PAS – H ierarchical M ultio bjective R outing considering 2 classes of S ervice with a P areto A rchive S trategy) follows.
The version without the Pareto archive, i.e., HMOR-S2, is equivalent to this one, without steps VII; VIII.11b ∙− Add to the archive ⋯; VIII.11b ∙ Else {and instructions therein}; VIII.11b ∙− Add to the archive ⋯; VIII.11b ∙ Else {and instructions therein}; X.
As for the ‘core’ algorithm MMRA-S2, it is basically an adaptation to the present model of the bi-objective constrained shortest path algorithm in [29] which is an extension of the algorithm in [14] to a multiservice environment.
HMOR-S2 PAS
-
I.
-
II.
Compute and W Q , B M m|Q for
-
III.
-
IV.
-
V.
Compute for
Compute for
-
VI.
max{W Q }←W Q , min{B M m|Q}←B M m|Q
and max{W B }←W B
-
VII.
Add to the archive
-
VIII.
For to n P a t h s=1
-
1.
For a p e=0 to a p e=1
-
(a)
If a p e=0, z A P R ←1.0
Else, z A P R ←0.01·n P a t h s
-
(b)
For s=1 to
-
i.
For n C y c l e s=1 to n C y c l e s=0
-
A.
Compute and or for
-
B.
Compute and order the values of the function ξ(f s ), with ξ(f s )=F L (f s ) if n C y c l e s=1 and if n C y c l e s=0
-
C.
Find the nPaths flows with lower value of ξ(f s )
-
D.
Compute with MMRA-S2 new candidate paths for the corresponding O-D pairs and define a new set of first and second choice paths for the service s, , according to the rules established for each service
-
E.
Compute for
Compute Bm s|Q, BM s|Q if or W B if for
Compute W Q , BM m|Q
-
F.
If then
-
If [(Bm s|Q< min{Bm s|Q} and BM s|Q< min{BM s|Q}) and (W Q > max{W Q } and BM m|Q< min{BM m|Q})] then
-
min{B m s|Q}←B m s|Q, min{B M s|Q}←B M s|Q
-
max{W Q }←W Q , min{B M m|Q}←B M m|Q –
-
Add to the archive (If it is already full, the priority regions of the solutions in the archive must be evaluated and the first solution found in the worst region of the archive should be removed first.)
-
Else,
-
If [(B m s|Q> min{B m s|Q} and B M s|Q> min{B M s|Q}) and (W Q < max{W Q } and B M m|Q> min{B M m|Q})] then
* (Discard )
-
Else,
* If there is at least one solution X in the archive for which [(Bm s|Q>Bm s|Q(X) and BM s|Q>BM s|Q(X)) and (W Q <W Q (X) and BM m|Q>BM m|Q(X))], i.e. X dominates in terms of the o.f. of interest,
† (Discard )
* Else ( and the solutions in the archive are non-dominated)
† If the archive is not full,
‡ Add to the archive
† Else
‡ Evaluate the priority regions of and the solutions in the archive;
‡ If is in the worst priority region
◦ (Discard )
‡ Else,
◦ Remove the first solution found in the worst region of the archive;
◦ Add to the archive
-
G.
Else ()
-
If [(W B > max{W B }) and (W Q > max{W Q } and BM m|Q< min{BM m|Q})] then
-
max{W B }←W B
-
max{W Q }←W Q , min{B M m|Q}←B M m|Q –
-
Add to the archive (If it is already full, the priority regions of the solutions in the archive must be evaluated and the first solution found in the worst region of the archive should be removed first.)
-
Else,
-
If [(W B <max{W B }) and (W Q <max{ W Q } and B M m|Q> min{B M m|Q})]
* (Discard )
-
Else,
* If there is at least one solution X in the archive for which [(W B <W B (X)) and (W Q <W Q (X) and BM m|Q>BM m|Q(X))], i.e. X dominates in terms of the o.f. of interest,
† (Discard )
* Else ( and the solutions in the archive are non-dominated)
† If the archive is not full,
‡ Add to the archive
† Else
‡ Evaluate the priority regions of and the solutions in the archive;
‡ If is in the worst priority region
◦ (Discard )
‡ Else,
◦ Remove the first solution found in the worst region of the archive;
◦ Add to the archive
-
H.
End of the cycle For (nCycles)
End of the cycle For (s)
End of the cycle For (ape)
End of the cycle For (nPaths)
-
IX.
If or then
-
1.
The best solution is .
-
X.
Else,
-
1.
Evaluate the priority regions of the solutions in the archive;
-
2.
The final solution is found in the best region of the archive, using a reference point-based procedure.
-
XI.
Compute the o.f. values for the final solution.
MMRA-S2
-
I.
For each link l k in the network, compute the path metrics: marginal implied costs and marginal blocking probabilities , where .
-
II.
Compute average values and .
-
III.
Compute the weights and .
-
IV.
For each link l k in the network, compute a cost of the link given by a weighted sum .
-
V.
Solve the problem using MPS [30], which allows for the computation of a set of κ paths for each flow for which the paths may change, ordered according to this cost function.
-
VI.
Identify the priority region to which each of the possible paths belongs to, where the first priority region is A, then B 2 and B 1, followed by C and finally D. The limits of the priority regions (Figure 4) are given by
where
-
VII.
The first choice route for each flow, r 1(f s ), is a non-dominated solution in the best possible priority region with the lowest value of implied cost.
-
VIII.
Consider all the arc-disjoint solutions from r 1(f s ).
-
IX.
The second choice route for each flow, r 2(f s ), is a non-dominated solution in the best possible priority region with the lowest value of implied cost.
References
Clímaco JCN, Craveirinha JMF: Multicriteria analysis in telecommunication network planning and design – Problems and issues. In Multiple Criteria Decision Analysis: State of the Art Surveys, International Series in Operations Research & Management Science, vol. 78. Edited by: Figueira J, Greco S, Ehrgott M. New York: Springer; 2005.
Clímaco JCN, Craveirinha JMF, Pascoal MMB: Multicriteria routing models in telecommunication networks – Overview and a case study. In Advances in Multiple Criteria Decision Making and Human Systems Management: Knowledge and Wisdom. Edited by: Shi Y, Olson DL, Stam A. Amsterdam: IOS Press; 2007.
Wierzbicki AP, Burakowski W: A conceptual framework for multiple-criteria routing in QoS IP networks. Int. Trans. Oper. Res 2011, 18(3):377–399. 10.1111/j.1475-3995.2010.00770.x
Craveirinha J, Girão-Silva R, Clímaco J: A meta-model for multiobjective routing in MPLS networks. Central Eur. J. Oper. Res 2008, 16(1):79–105. 10.1007/s10100-007-0044-9
Girão-Silva R, Craveirinha J, Clímaco J: Hierarchical multiobjective routing model in Multiprotocol Label Switching networks with two service classes – a Pareto archive strategy. Eng. Optimization 2012, 44(5):613–635. 10.1080/0305215X.2011.591792
Steuer RE: Multiple Criteria Optimization: Theory, Computation and Application. Probability and Mathematical Statistics. New York: John Wiley & Sons; 1986.
Girão-Silva R, Craveirinha J, Clímaco J: Hierarchical multiobjective routing in MPLS networks with two service classes - Report on a simulation case study. Research Report 11/2011 (ISSN 1645–2631), INESC-Coimbra. 2011.
Bouyssou D: Modelling inaccurate determination, uncertainty, imprecision using multiple criteria. In Improving Decision, Making in Organisations. LNEMS, vol. 335. Edited by: Lockett AG, Islei G. Berlin Heidelberg: Springer; 1989.
Mitra D, Morrison JA, Ramakrishnan KG: Optimization and design of network routing using refined asymptotic approximations. Perform. Eval 1999, 36–37: 267–288.
Kaufman JS: Blocking in a shared resource environment. IEEE Trans. Commun 1981, COM-29(10):1474–1481.
Roberts JW: Teletraffic models for the Telecom 1 integrated services network. In Proceedings of 10th International Teletraffic Congress. Montreal; 1983.
Mitra D, Morrison JA: Erlang capacity and uniform approximations for shared unbuffered resources. IEEE/ACM Trans. Netw 1994, 2(6):558–570. 10.1109/90.365417
Craveirinha J, Girão-Silva R, Clímaco J, Martins L: A hierarchical multiobjective routing model for MPLS networks with two service classes. In Revised Selected Papers of the 23rd IFIP TC7 Conference on System Modeling and Optimization, Cracow, July 23–27 2007. IFIP Advances in Information and Communication Technology, vol. 312. Edited by: Korytowski A, Malanowski K, Mitkowski W, Szymkat M. New York: Springer; 2009.
Craveirinha J, Martins L, Gomes T, Antunes CH, Clímaco JN: A new multiple objective dynamic routing method using implied costs. J. Telecommunications Inf. Technol 2003, 3: 50–59.
Martins L, Craveirinha J, Clímaco JN, Gomes T: Implementation and performance of a new multiple objective dynamic routing method for multiexchange networks. J. Telecommunications Inf. Technol 2003, 3: 60–66.
Girão-Silva R, Craveirinha J, Clímaco J: Hierarchical multiobjective routing in Multiprotocol Label Switching networks with two service classes - a heuristic solution. Int. Trans. Oper. Res 2009, 16(3):275–305. 10.1111/j.1475-3995.2009.00669.x
Akimaru H, Kawashima K: Teletraffic: Theory and Applications, Telecommunication Networks and Computer Systems. New York: Springer; 1993.
Tralhão L, Craveirinha J, Paixão J: A study on a stochastic system with multiple MMPP inputs subject to access functions. In New Progress in Probability and Statistics - 4th International Symposium on Statistics of the Base Country. Zeist: VSP - International Publishers; 1994.
Kelly FP: Blocking probabilities in large circuit-switched networks. Adv. Appl. Probability 1986, 18(2):473–505. 10.2307/1427309
Sayed HME, Mahmoud MS, Bilal AY, Bernussou J: Adaptive alternate-routing in telephone networks: Optimal and equilibrium solutions. Inf. Decis. Technol 1988, 14(1):65–74.
Durbach IN, Stewart TJ: Modeling uncertainty in multi-criteria decision analysis. Eur. J. Oper. Res 2012, 223: 1–14. 10.1016/j.ejor.2012.04.038
Clímaco JCN, Craveirinha JMF, Pascoal MMB: An automated reference point-like approach for multicriteria shortest path problems. J. Syst. Sci. Syst. Eng 2006, 15(3):314–329. 10.1007/s11518-006-5015-5
Ash GR: Traffic Engineering and QoS Optimization of Integrated Voice & Data Networks. Morgan Kaufmann: Elsevier; 2007.
Mitra D, Ramakrishnan KG: Techniques for traffic engineering of multiservice, multipriority networks. Bell Labs Tech. J 2001, 6(1):139–151.
Erbas SC, Erbas C: A multiobjective off-line routing model for MPLS networks. In Proceedings of the 18th, International Teletraffic Congress (ITC-18). Edited by: Charzinski J, Lehnert R, Tran-Gia P. Amsterdam, Berlin: Elsevier; 2003.
Banks J, Carson II JS: Discrete-Event System Simulation. International Series in Industrial and Systems Engineering. Upper Saddle River: Prentice-Hall; 1984.
Awduche D, Chiu A, Elwalid A, Widjaja I, Xiao X: Overview and principles of Internet traffic engineering. RFC 3272, Network Working Group. The Internet Engineering Task Force. California: ; 2002.
Leland W, Taqqu M, Willinger W, Wilson D: On the self-similar nature of Ethernet traffic (Extended version). IEEE/ACM Trans. Netw 1994, 2(1):1–15. 10.1109/90.282603
Martins L, Craveirinha J, Clímaco J: A new multiobjective dynamic routing method for multiservice networks: modelling and performance. Comput. Manage. Sci 2006, 3(3):225–244. 10.1007/s10287-006-0014-z
Gomes T, Martins L, Craveirinha J: An algorithm for calculating k shortest paths with a maximum number of arcs. Investigação Operacional 2001, 21: 235–244.
Acknowledgements
The authors would like to thank the anonymous referees for their helpful comments and remarks. This work was financially supported by programme COMPETE of the EC Community Support Framework III and cosponsored by the EC fund FEDER and national funds (FCT - PTDC/EEA-TEL/101884/2008 and PEst-C/EEI/UI0308/2011).
Author information
Authors and Affiliations
Corresponding author
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Girão-Silva, R., Craveirinha, J. & Clímaco, J. Stochastic hierarchical multiobjective routing model in MPLS networks with two service classes: an experimental study on imprecision and uncertainty issues. J. Uncertain. Anal. Appl. 2, 3 (2014). https://doi.org/10.1186/2195-5468-2-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2195-5468-2-3



 and
and