- Research
- Open access
- Published:
Importance Index of Components in Uncertain Reliability Systems
Journal of Uncertainty Analysis and Applications volume 4, Article number: 7 (2016)
Abstract
Importance measure is an index for estimating the importance of an individual component or a group of components in a reliability system. So far, the importance measures for components in stochastic reliability systems have been investigated. In order to calculate the importance of a component or a group of components in an uncertain reliability system, this paper proposes a new concept of importance index. Some formulas are given to calculate the importance index of a component and a group of components in an uncertain reliability system. Then, some special types of uncertain reliability systems such as uncertain series, parallel, parallel-series, series-parallel, bridge, and k-out-of-n systems are studied.
Introduction
The subject of the importance measure of components in a stochastic system has been developing for many years. In the late 1940s and early 1950s, reliability of a stochastic system was first presented and applied to some fields such as communication, transportation, and military systems. Along with the design for reliability, Birnbaum [2] proposed the concept of importance measure of components in a stochastic coherent reliability system. In reliability engineering, the importance measure is an index for estimating the relative importance of an individual component or a group of components in a stochastic system. Birnbaum classified the importance measure into three classes which are structure importance measure, reliability importance measure, and lifetime importance measure. Fussell [5] presented another importance measure for a component which is nonproportional to importance measure defined by Birnbaum [2]. Barlow and Proschan [1] came up with a type of time-independent lifetime importance measure of components in a stochastic system, which described the importance of a functioning component to the whole system. Natvig [26] proposed another type of time-independent lifetime importance to evaluate the possibility of a failing component leading to the failure of whole stochastic system. Recently, many researchers have applied importance measures into some specific stochastic reliability systems, such as Derman et al. [4], Kuo et al. [13], Kuo and Zuo [14], Kuo and Zhu [15] and Jalali et al. [12].
As is well known, randomness is a type of indeterminacy, which is modeled by probability theory. Probability theory has developed steadily for many years and has been widely applied in science and engineering. We usually make a basic assumption that the estimated probability and the long-run cumulative frequency are close enough when using probability theory. This implies that we should obtain a lot of observed data. However, observed data cannot always be obtained for technical or some other reasons, so we have to rely on domain experts to evaluate the belief degrees about the chances that the possible events may happen. Liu [25] showed that human beings usually estimate a much wider range of values than the object actually takes. That is, there is a large gap between the belief degrees estimated by human beings and the real frequencies. Hence, the belief degree cannot be modeled by probability measure. Some convincing examples may be found in Liu [24]. Naturally, we should find other mathematical tools to deal with the belief degree.
To deal with the experts’ belief degrees, Liu [17] founded uncertainty theory in 2007, and Liu [19] refined it in 2009 with presenting the product uncertain measure axiom for dealing with the operations of uncertain variables. Some fundamental concepts were presented by Liu [17], such as uncertain measure for indicating the belief degree, uncertain variable for modeling the uncertain quantity, and uncertainty distribution for describing an uncertain variable. Peng and Iwamura [27] studied a sufficient and necessary condition for a real function being the uncertainty distribution of an uncertain variable. Additionally, Liu [19] raised a concept of independence for uncertain variables. For ranking uncertain variables, Liu [17] proposed a concept of expected value operator. Up to now, uncertainty theory has been successfully applied to many problems such as, uncertain programming (Liu [20], Gao et al. [11]), uncertain risk and reliability analysis (Liu [22]), uncertain propositional logic (Li and Liu [16]), uncertain set (Liu [23]), uncertain process (Liu [18], Chen [3]), uncertain field (Gao and Chen [7]), uncertain finance (Liu [19]), uncertain differential equation (Liu [18], Gao [6]), and uncertain graph (Gao et al. [9], Gao and Qin [10]).
Based on uncertainty theory, Liu [21] investigated the system reliability, introducing a definition of reliability index and providing some useful formulas to calculate the reliability index. Then, Gao et al. [8] studied the reliability index of uncertain k-out-of-n systems. By the inspiration of importance measure associated with components in a stochastic system, a new concept of importance index for an individual component or a group of components in an uncertain reliability systems is introduced as a mathematical tool to model the importance of such a component in this paper.
The rest of this paper is organized as follows. Some basic concepts and properties with respect to uncertain variables and Boolean system are reviewed in the section “Preliminaries”. We devote the section “Importance Index of Individual Component” to presenting a new concept of importance index for an individual component in an uncertain reliability system and taking some examples to show how to calculate the importance index of a component. In the section “Importance Index of Group of Components,” a concept of importance index for a group of components in an uncertain reliability system is presented and some examples are also given to show how to calculate the importance index of a group of components. In the section “Main Results,” we provide some formulas to calculate the importance index of a component and a group of components in an uncertain reliability system. Finally, we make a summary of the full paper in the section “Conclusion”.
Preliminaries
In this section, we introduce some fundamental concepts and properties concerning uncertain variables and Boolean systems.
Uncertainty Variable
Let Γ be a nonempty set and \(\mathcal {L}\) a σ-algebra over Γ. Each element Λ in \(\mathcal {L}\) is called an event. To deal with belief degree on the possibility of each event rationally, a concept of uncertain measure  was given by Liu [17, 19] as a set function satisfying the following axioms:
was given by Liu [17, 19] as a set function satisfying the following axioms:
-
Axiom 1.
(Normality)
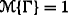 for the universal set Γ;
for the universal set Γ; -
Axiom 2.
(Duality)
 for each event Λ;
for each event Λ; -
Axiom 3.
(Subadditivity)
For every countable sequence of events Λ 1,Λ 2,⋯, we have
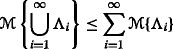
-
Axiom 4.
(Product Axiom) Let
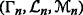 be uncertainty spaces for n=1,2,⋯ For any events Λ
n
chosen from \(\mathcal {L}_{n}\), the uncertain measure
be uncertainty spaces for n=1,2,⋯ For any events Λ
n
chosen from \(\mathcal {L}_{n}\), the uncertain measure  satisfies
satisfies
Definition 1
(Liu [
17
]) An uncertain variable is a measurable function ξ from an uncertainty space  to a set of real numbers. That is, for any Borel set B of real numbers, the set
to a set of real numbers. That is, for any Borel set B of real numbers, the set
is an event.
The uncertain variables ξ 1,ξ 2,⋯,ξ n are said to be independent if

holds for any Borel sets B
1,B
2,⋯,B
n
. For an uncertain variable ξ, the function  is called its uncertainty distribution.
is called its uncertainty distribution.
Theorem 1
(Liu [ 21 ]) Assume that ξ 1,ξ 2,⋯,ξ n are some independent uncertain variables with continuous uncertainty distributions Φ 1,Φ 2,⋯,Φ n , respectively. Then, for an increasing function f(x 1,x 2,⋯,x n ), the uncertain variable
has an uncertainty distribution
For ranking uncertain variables, the concept of expected value was proposed by Liu [17] in the following.
Definition 2
(Liu [17]) Let ξ be an uncertain variable. Then, the expected value of ξ is defined by

provided that at least one of the two integrals is finite.
Theorem 2
(Liu [17]) Let ξ be an uncertain variable with uncertainty distribution Φ. If the expected value exists, then
Boolean System
A Boolean function maps {0,1}n to {0,1}. For example,
is a Boolean function, where x 1,x 2,x 3 take values either 0 or 1. If an uncertain variable takes values either 0 or 1, then it is said to be Boolean. For example,
is a Boolean uncertain variable, where b is a number between 0 and 1.
Theorem 3
(Liu [21]) Assume that ξ 1,ξ 2,⋯,ξ n are independent Boolean uncertain variables, i.e.,
for i=1,2,⋯,n. Then, for a Boolean function f(x 1,x 2,⋯,x n ), the Boolean uncertain variable ξ=f(ξ 1,ξ 2,⋯,ξ n ) satisfies

where x i take values either 0 or 1 and ν i are defined by
for i=1,2,⋯,n, respectively.
Assume that ξ is a Boolean system with components ξ 1,ξ 2,⋯,ξ n . Then, a Boolean function f is called a structure function of ξ if
Definition 3
(Liu [22]) If the Boolean system is uncertain, the reliability index is the uncertain measure that the system is functioning, i.e.,

Theorem 4
(Liu [22]) Assume that a Boolean system has uncertain components ξ 1,ξ 2,⋯,ξ n and has a structure function f. If ξ 1,ξ 2,⋯,ξ n are independent and have reliabilities b 1,b 2,⋯,b n , respectively, then the reliability index is
where ξ i take values either 0 or 1, and ν i are defined by
for i=1,2,⋯,n, respectively.
Example 1
For an uncertain series system in Fig. 1, the structure function is
If ξ 1,ξ 2,⋯,ξ n are independent and have reliabilities b 1,b 2,⋯,b n , respectively, then the reliability index is
Example 2
For an uncertain parallel system in Fig. 2, the structure function is
If ξ 1,ξ 2,⋯,ξ n are independent and have reliabilities b 1,b 2,⋯,b n , respectively, then the reliability index is
Example 3
For an uncertain k-out-of-n system containing n components which functions if and only if at least k components function, the structure function is
If ξ 1,ξ 2,⋯,ξ n are independent and have reliabilities b 1,b 2,⋯,b n , respectively, then the reliability index is
Importance Index of Individual Component
The subject of importance measure for an individual component in a stochastic system has been developing for a long time. For investigating the importance of an individual component in an uncertain system, we present a new concept of importance index as follows.
Definition 4
Assume an uncertain Boolean system has components ξ 1,ξ 2,⋯,ξ n and a structure function f. Then, the importance index of Component i is

The important index of Component i is the difference between the reliabilities of the uncertain system in two different cases: the former case is that Component i functions and the latter case is that Component i fails.
Remark 1
Importance index of a component in an uncertain system actually means the degree of importance of a component to the whole system. The higher the importance index of a component is, the more important it is to the whole system. For example, if the important index of a component is one, then it indicates that this component is indispensable to the system; if the important index of a component is zero, then it shows that this component is superfluous to the system. That implies that if we want to improve the reliability of a system, we have to ensure the normal operation of the components with higher importance index.
Important index can be applied into various fields to evaluate the relative importance of some components in an uncertain system. Their absolute values might not be as significant as their relative rankings. For example, in a large and complex pipeline network, there are pipelines without statistical information. These pipelines are used to transport various fluids from production sites to consumption ones and they are also essential components of such transportation network. The safe handling is of great importance due to the serious consequences of the faulty operations, such as the cracking of the welding seam and hole corrosion. So we should find a highly reliable route as well as the key components in such a route. That requires us to calculate the relative importance of the components in this pipeline network. Additionally, consider a complex electric vehicle which contains 100 powerful batteries without statistical information. This electric vehicle is required to last a long time and the power is significantly reduced if more than eight or nine batteries fail, which can be regarded as a 92/91-out-of-100 system. Thus, we should know which battery is relatively important. That asks us to know the importance index of the components in this electric battery system.
Next, we will use some specifically numerical examples to illustrate how to calculate the importance index of a component in an uncertain system.
Example 4
(Series System) Consider an uncertain series system in Fig. 3 with 4 components ξ 1,ξ 2,ξ 3,ξ 4, whose structure function is
Suppose ξ 1,ξ 2,ξ 3,ξ 4 are independent and have reliabilities 0.2,0.7,0.9,0.4 in uncertain measure, respectively. Then, it follows from Definition 4 that the importance index of Component 3 is

Example 5
(Parallel System) Consider an uncertain parallel system in Fig. 4 with 4 components ξ 1,ξ 2,ξ 3,ξ 4, whose structure function is
Suppose ξ 1,ξ 2,ξ 3,ξ 4 are independent and have reliabilities 0.2,0.7,0.9,0.4 in uncertain measure, respectively. Then, it follows from Definition 4 that the importance index of Component 3 is

Example 6
(Parallel-Series System) Consider an uncertain parallel-series system in Fig. 5 with 4 components ξ 1,ξ 2,ξ 3,ξ 4. Assume each path functions if and only if its components function, and the system functions if and only if there is at least one functioning path. Then, the structure function of the parallel-series system is
Suppose ξ 1,ξ 2,ξ 3,ξ 4 are independent and have reliabilities 0.2, 0.7, 0.9, 0.4 in uncertain measure, respectively. Then, it follows from Definition 4 that the importance index of Component 3 is

Example 7
(Series-Parallel System) Consider an uncertain series-parallel system in Fig. 6 with 4 components ξ 1,ξ 2,ξ 3,ξ 4. Assume each path functions if and only if its components function, and the system functions if and only if there is at least one functioning path. Then, the structure function of the series-parallel system is
Suppose ξ 1,ξ 2,ξ 3,ξ 4 are independent and have reliabilities 0.2, 0.7, 0.9, 0.4 in uncertain measure, respectively. Then, it follows from Definition 4 that the importance index of Component 3 is

Example 8
(Bridge System) Consider a bridge system in Fig. 7 with 5 components ξ 1,ξ 2,ξ 3,ξ 4,ξ 5. Assume each path functions if and only if its components function, and the system functions if and only if there is at least one functioning path. Then, the structure function of the bridge system is
Suppose ξ 1,ξ 2,ξ 3,ξ 4,ξ 5 are independent and have reliabilities 0.2,0.7,0.9,0.8,0.4 in uncertain measure, respectively. Now, we will calculate the importance index of Component 3. Since
we have

according to Theorem 4. Then, it follows from Definition 3 that the reliability index of the system when Component 3 functions is

and the reliability index of the system when Component 3 fails is

Thus, the importance index of Component 3 is

according to the Definition 4.
The above examples clearly showed that the importance index of an individual component is related to the structure of the system.
Importance Index of Group of Components
Sometimes, we need to know the importance of a group of components in an uncertain reliability system. Now, we give a concept of importance index for a group of components in an uncertain reliability system in this section.
Definition 5
Assume an uncertain Boolean system has components ξ 1,ξ 2,⋯,ξ n and a structure function f. Then, the importance index of a group of Components i 1,i 2,⋯,i l is

The important index of the group of Components \(\xi _{i_{1}},\xi _{i_{2}},\cdots,\xi _{i_{l}}\) is the difference between the reliabilities of the uncertain system in two different cases: the former case is that Components \(\xi _{i_{1}},\xi _{i_{2}},\cdots,\xi _{i_{l}}\) function, and the latter case is that Components \(\xi _{i_{1}},\xi _{i_{2}},\cdots,\xi _{i_{l}}\) fail.
Example 9
(Series System) Consider the uncertain series system in Example 4. Then, it follows from Definition 5 that the importance index of Components 1 and 3 is

Example 10
(Parallel System) Consider the uncertain parallel system in Example 5. Then, it follows from Definition 5 that the importance index of Components 1 and 3 is

Example 11
(Parallel-Series System) Consider the uncertain parallel-series system in Example 6. Then, it follows from Definition 5 that the importance index of Components 1 and 3 is

Example 12
(Series-Parallel System) Consider the uncertain series-parallel system in Example 7. Then, it follows from Definition 5 that the importance index of Components 1 and 3 is

Example 13
(Bridge System) Consider the bridge system in Example 8. Now, we begin to calculate the importance index of Components 1 and 3. Since
we have

according to Theorem 4. Then, it follows from Definition 3 that the reliability index of the system when Components 1 and 3 function is

and the reliability index of the system when Components 1 and 3 fail is

Thus, the importance index of Components 1 and 3 is

according to the Definition 3.
The above examples clearly showed that the importance of a group of components is related to the structure of the system.
Main Results
In this section, we propose some formulas to calculate the importance index for a component or a group of components in an uncertain reliability system.
Formulas on Individual Component
Firstly, we give a formula to calculate the importance index for an individual component in an uncertain reliability system.
Theorem 5
Suppose a Boolean system has components ξ 1,ξ 2,⋯,ξ n , and has a structure function f. If the components ξ 1,ξ 2,⋯,ξ n are independent and their reliabilities are a 1,a 2,⋯,a n , respectively, then the importance index of Component i is
where
and
Here, ξ j take values either 0 or 1 and ν j are defined by
for j=1,2,⋯,n, respectively.
Proof
This theorem follows from Theorem 4 directly. □
Corollary 1
Consider an uncertain series system with independent components ξ 1,ξ 2,⋯,ξ n whose reliabilities are a 1,a 2,⋯,a n , respectively. Note that the structure function has a Boolean form
Then, the importance index of Component i is
Proof
If Component i functions, then the reliability index of the system is

And if Component i fails, then the reliability index of the system is

Thus, it follows from Theorem 5 that the importance index of Component i is
The proof is complete. □
Corollary 2
Consider an uncertain parallel system with independent components ξ 1,ξ 2,⋯,ξ n whose reliabilities are a 1,a 2,⋯,a n , respectively. Note that the structure function has a Boolean form
Then, the importance index of Component i is
Proof
If Component i functions, then the reliability index of the system is

And if Component i fails, then the reliability index of the system is

Thus, it follows from Theorem 5 that the importance index of Component i is
The proof is complete. □
Corollary 3
Consider a k-out-of-n system with independent uncertain components ξ 1,ξ 2,⋯,ξ n whose reliabilities are a 1,a 2,⋯,a n , respectively. Note that the structure function has a Boolean form
Then, the importance index of Component i is
Here, we set 0− max[a 1,⋯,a i−1,a i+1⋯,a n ]=1 and n− max[a 1,⋯,a i−1,a i+1⋯,a n ]=0.
Proof
If Component i functions, then the reliability index of the system is

and if Component i fails, then the reliability index of the system is

Thus, it follows from Theorem 5 that the importance index of Component i is
The proof is complete. □
Formulas on Group of Components
Sometimes, we need to know the importance index of a group of components in an uncertain reliability system. Now, we give a formula to calculate the importance index of a group of components in an uncertain reliability system.
Theorem 6
Suppose a Boolean system has components ξ 1,ξ 2,⋯,ξ n , and has a structure function f. If components ξ 1,ξ 2,⋯,ξ n are independent, and their reliabilities are a 1,a 2,⋯,a n , respectively, then the importance index of the group of Components i 1,i 2,⋯,i l is
where
and
Here, ξ j take values either 0 or 1, and ν j are defined by
for j=1,2,⋯,n, respectively.
Corollary 4
Consider an uncertain series system with independent components ξ 1,ξ 2,⋯,ξ n whose reliabilities are a 1,a 2,⋯,a n , respectively. Note that the structure function has a Boolean form
Then, the importance index of the group of Components i 1,i 2,⋯,i l is
Proof
If Components i 1,i 2,⋯,i l function, the reliability index of the system is

And if Components i 1,i 2,⋯,i l fail, the reliability index of the system is

Thus, it follows from Theorem 6 that the importance index of Components i 1,i 2,⋯,i l is
The proof is complete. □
Corollary 5
Consider an uncertain parallel system with independent components ξ 1,ξ 2,⋯,ξ n whose reliabilities are a 1,a 2,⋯,a n , respectively. Note that the structure function has a Boolean form
Then, the importance index of the group of Components i 1,i 2,⋯,i l is
Proof
If Components i 1,i 2,⋯,i l function, then the reliability index of the system is

And if Components i 1,i 2,⋯,i l fail, then the reliability index of the system is

Thus, it follows from Theorem 6 that the importance index of the group of Components i 1,i 2,⋯,i l is
The proof is complete. □
Corollary 6
Consider a k-out-of-n system with independent uncertain components ξ 1,ξ 2,⋯,ξ n whose reliabilities are a 1,a 2,⋯,a n , respectively. Note that the structure function has a Boolean form
Then, the importance index of the group of components i 1,i 2,⋯,i l is
Here, we set
and
Proof
If Components i 1,i 2,⋯,i l function, then the reliability index of the system is

and if Components i 1,i 2,⋯,i l fail, then the reliability index of the system is

Thus, it follows from Theorem 6 that the importance index of Component i 1,i 2,⋯,i l is
The proof is complete. □
Conclusion
Inspired by the investigation of importance measure for components in a stochastic reliability system, this paper put forward a new concept of importance index for an individual component or a group of components in an uncertain reliability system. Several systems including series, parallel, parallel-series, series-parallel, and bridge systems are investigated to illustrate this concept for a component or a group of components. Then, some formulas were derived to calculate the importance index. Based on this results, we would study the lifetime importance index of a component in an uncertain system in the future.
References
Barlow, RE, Proschan, F: Importance of system components and fault tree events. Stoch. Process. Appl. 3(2), 153–173 (1975).
Birnbaum, ZW: On the importance of different components in a multicomponent system. J. Multivar. Anal. 2, 581–592 (1969).
Chen, XW: Variation analysis of uncertain stationary independent increment processes. Eur. J. Oper. Res. 222(2), 312–316 (1969).
Derman, C, Lieberman, GJ, Ross, SM: On the consecutive-k-out-of-n: F system. IEEE Trans. Reliab. 31(1), 57–63 (1982).
Fussell, JB: How to hand-calculate system reliability and safety characteristics. IEEE Trans. Reliab. 24(3), 169–174 (1975).
Gao, R: Milne method for solving uncertain differential equations. Appl. Math. Comput. 274, 774–785 (2016).
Gao, R, Chen, XW: Some concepts and properties of uncertain fields. J. Intell. Fuzzy Syst. doi:10.3233/JIFS-16314.
Gao, Y, Gao, R, Yang, LX: Order statistics of uncertain variables. J. Uncertain. Anal. Appl. 3(Article. 1) (2015).
Gao, Y, Yang, LX, Shukai, Li, Samarjit, Kar: On distribution function of the diameter in uncertain graph. Inf. Sci. 296, 61–74 (2015).
Gao, Y, Qin, ZF: On computing the edge-connectivity of an uncertain graph. IEEE Trans. Fuzzy Syst. 24(4), 981–991 (2016).
Gao, Y, Yang, LX, Shukai, Li: Uncertain models on railway transportation planning problem. Appl. Math. Model. 40, 4921–4934 (2016).
Jalali, A, Hawkes, AG, Cui, LR, Hwang, FK: The optimal consecutive-k-out-of-n: G line for n≤2k. J. Plan. Infer. 128, 281–287 (2005).
Kuo, W, Zhang, W, Zuo, MJ: A consecutive k-out-of-n: G system: the mirror image of a consecutive k-out-of-n: F system. IEEE Trans. Reliab. 39(2), 244–253 (1990).
Kuo, W, Zuo, MJ: Optimal reliability modeling: principles and applications. Wiley, New York (2003).
Kuo, W, Zhu, XY: Importance measures in reliability, risk, and optimization: principles and applications. Wiley, London (2012).
Li, X, Liu, B: Hybrid logic and uncertain logic. J. Uncertain Syst. 3(2), 83–94 (2009).
Liu, B: Uncertainty theory. 2nd ed. Springer-Verlag, Berlin (2007).
Liu, B: Fuzzy process, hybrid process and uncertain process. J. Uncertain Syst. 2(1), 3–16 (2008).
Liu, B: Some research problems in uncertainty theory. J. Uncertain Syst. 3(1), 3–10 (2009).
Liu, B: Theory and practice of uncertain programming. 2nd ed. Springer-Verlag, Berlin (2009).
Liu, B: Uncertainty theory: a branch of mathematics for modeling human uncertainty. Springer-Verlag, Berlin (2010).
Liu, B: Uncertain risk analysis and uncertain reliability analysis. J. Uncertain Syst. 4(3), 163–170 (2010).
Liu, B: Uncertain set theory and uncertain inference rule with application to uncertain control. J. Uncertain Syst. 3(4), 243–251 (2010).
Liu, B: Why is there a need for uncertainty theory?J. Uncertain Syst. 6(Article. 1), 3–10 (2012).
Liu, B: Uncertainty theory. 4th ed. Springer-Verlag, Berlin (2015).
Natvig, B: A suggestion of a new measusure of imporance of system component. Stoch. Process. Appl. 9(3), 319–330 (1979).
Peng, ZX, Iwamura, K: A sufficient and necessary condition of uncertainty distribution. J. Interdiscip. Math. 13(3), 277–285 (2010).
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant Nos. 61573210 and 61403360).
Authors’ contributions
RG carried out the study in the paper and drafted the first version of the manuscript. RG and KY designed the framework together. KY revised the first version of the manuscript. Both authors read and approved the final manuscript.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gao, R., Yao, K. Importance Index of Components in Uncertain Reliability Systems. J. Uncertain. Anal. Appl. 4, 7 (2016). https://doi.org/10.1186/s40467-016-0047-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40467-016-0047-y
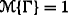 for the universal set Γ;
for the universal set Γ; for each event Λ;
for each event Λ;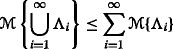
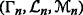 be uncertainty spaces for n=1,2,
be uncertainty spaces for n=1,2, satisfies
satisfies






