Pricing Decision in a Two-Echelon Supply Chain with Competing Retailers Under Uncertain Environment

Abstract

This paper explores a supply chain pricing competition problem in a two-echelon supply chain with one manufacturer and two competing retailers. The manufacturing costs, sales costs, and market bases are all characterized as uncertain variables whose distributions are estimated by experts’ experienced data. In consideration of channel members’ different market powers, three decentralized game models are employed to explore the equilibrium behaviors in corresponding decision circumstances. How the channel members should choose their most profitable pricing strategies in face of uncertainties is derived from these models. Numerical experiments are conducted to examine the effects of power structures and parameters’ uncertain degrees on the pricing decisions of the members. The results show that the existence of dominant powers in the supply chain will increase the sales prices and reduce the profit of the whole supply chain. It is also found that the supply chain members may benefit from higher uncertain degrees of their own costs while the other supply chain members will gain less profits. Additionally, the results demonstrate that the uncertainty of the supply chain will make end consumers pay more. Some other interesting managerial highlights are also obtained in this paper.

Introduction

In this paper, we explore a pricing decision problem in a decentralized supply chain with competing retailers under uncertainty. In such supply chains, costs and demands may be subject to some inherent indeterministic factors, such as material cost changes, labor costs, technology improvements, and customer incomes. It is necessary to identify distributions of these parameters, which are essential for supply chain managers when they make decisions, e.g., choosing prices, determining production quantities, choosing ordering quantities, and adding investment. Theoretically, we can collect enough samples to estimate distributions of these parameters before we make decisions. However, products, especially high-tech products, e.g., smartphones, PCs, and other digital devices, have been rapidly updated recently. The costs and demands for these new products are usually the lack of historical data, or we can collect enough data, but these data may not be applicable due to the dynamic environment. Practically, domain experts’ experience data (belief degrees) are often applied to estimate the distributions in such cases. Nevertheless, some surveys have shown that human beings (even the most experienced experts) usually estimate a much wider range of values than the object actually takes. It makes belief degrees behave quite different from frequency, indicating that human belief degrees given by managers and experts should not be treated as random variables or fuzzy variables [1]. Instead, based on normality, duality, subadditivity, and product axioms, uncertainty theory, initiated by Liu [2] and refined by Liu [3], can be introduced to deal with parameters estimated by human belief degrees.

The goal of this paper is to study supply chain pricing problems with uncertainty theory. Our work mainly focuses on equilibrium behaviors of the decentralized supply chain with one common manufacturer (upstream member) and duopoly retailers (downstream members) under uncertainty. A supply chain with competing retailers is not uncommon in the real industry world. For instance, smartphone producers distribute their products through both traditional retailers and online retailers. How should the supply chain managers choose the most profitable price policies with experts’ estimations? What effects might the uncertain degrees of the parameters have on the supply chain members’ pricing decisions and expected profits? Additionally, we assume that the manufacturer determines the wholesale prices and the two retailers compete for end consumers by choosing their own sales prices. The decision sequence is mainly decided by the power structures of the supply chain. In some supply chains, the manufacturers (like Intel and Microsoft) often play a more powerful role with regard to the other channel members. In some other chains, the retailers (like Warmart and Carrefour) who are much bigger than most manufacturers often hold the dominant power. While in another type of supply chain, no absolute dominance exists between different members and each member holds the same power. How would these various power structures affect the performance of the supply chain?

In order to answer these questions, three decentralized pricing models based on uncertainty theory and game theory are built. Then, the corresponding closed-form equilibrium solutions are derived from these models. Afterwards, numerical experiments are conducted to analyze the equilibrium behaviors of the supply chain under different power structures and uncertain settings. It is found that the manufacturer can benefit from a higher uncertain degree of the manufacturing cost, meanwhile, the retailers will gain less profits. Similarly, when the uncertain degree of the sales costs increases, the retailers can make more profits while the manufacture will gain less. Additionally, the uncertainty of the supply chain will make end consumers pay more. Some other interesting managerial highlights are also obtained in this paper.

The remainder of this paper is organized as follows: some related literatures are presented in the “Literature Review” section. Some basic concepts and properties with respect to uncertain variable are reviewed in the “Preliminaries” section. Some useful notations and necessary assumptions are discussed in the “Problem Description” section. Three models are employed to derive the equilibria under three possible scenarios in the “Models and Solution Approaches” section. In the “Numerical Experiments” section, numerical experiments are applied to examine the equilibrium behaviors of the supply chain members. Some conclusions and possible extensions are discussed in the “Conclusions” section.

Literature Review

By now, the pricing competition problem in decentralized supply chains, initiated in 1980s [4, 5], has been well studied by both scholars and practitioners. Most of these researches on the pricing competition problem focus on the following four structures: monopoly common retailer structure [6–8], chain-to-chain structure [4, 9, 10], dual channel structure [11–14], and monopoly common manufacturer structure, which is studied in this paper. The research on the monopoly common manufacturer structure was initiated by Ingene and Parry [15], considering a coordination problem in a supply chain where a manufacturer sells its products through competing retailers. Ingene and Parry [16] demonstrated that the manufacturer can generally obtain more profits by setting a unique two-part tariff wholesale pricing policy. For pricing competition, Yang et al.[17] considered a pricing problem in a two-echelon supply chain with a manufacturer who supplies a single product to two competing retailers. Assuming that the manufacturer acts as a Stackelberg leader, they explored the effects of the retailers’ Bertrand and Collusion behaviors on the performance of the supply chain. Wu et al.[18] investigated the pricing decision in this monopoly common manufacturer channel structure and built six noncooperative models where the two retailers play Stackelberg or Bertrand games under three possible power structures. Besides, Huang et al.[19] considered a pricing competition and cooperation problem in a supply chain with one common manufacturer and duopoly retailers and explored the conditions under which the retailers can benefit from their collusion behaviors.

The work above typically focused on deterministic demands and costs. In fact, the real world exists many indeterminate factors which cannot be ignored when making pricing decisions. Thus, one important tendency is to explore the pricing competition problem under environments with indeterminate factors, namely randomness, fuzziness, or uncertainty. For instance, Bernstein and Federgruen [20] investigated the equilibrium behaviors of decentralized supply chains with competing retailers under random demand and designed some contractual arrangements between the parties that allow the decentralized chain to perform like a centralized one. Xiao and Yang [21] studied a price and service competition of two supply chains with risk-averse retailers under stochastic demand. They also analyzed the impacts of the retailer’s risk sensitivity on the manufacturers’ equilibrium strategies. Wu et al.[9] considered a joint pricing and quantity competition between two separate supply chains in random environment and explored the effects of randomness on the equilibrium behaviors of the supply chain members. Shi et al.[22] utilized a game-theory-based framework to formulate the power in a supply chain and examined how power structure and demand indeterminacy affect the supply chain members’ performances. Mahmoodi and Eshghi [23] studied this pricing problem in duopoly supply chains with stochastic demand and explored the effects of competition and demand indeterminacy intensity on the equilibria of the structures by a numerical experiment. Li et al.[24] studied the pricing and remanufacturing decision problem with random yield and demand.

More recently, fuzzy set theory has been introduced to the pricing decision problems. Zhou et al.[25] considered the pricing decision problem in a supply chain which consists of a manufacturer and a retailer in fuzzy environment. Zhao et al.[26] and Sang [27] studied the pricing problem on two substitutable products in a supply chain with different structures in which the manufacturing costs and consumer demands were described by fuzziness. Specially, Liu and Xu [28] and Ke et al.[29] studied the pricing problem in a fuzzy supply chain consisting of one manufacturer and two competitive retailers.

To the best of our knowledge, there are little researches on the pricing decision problem with competing retailers under uncertain settings. Differing from the literatures above, this paper addresses the pricing equilibria under circumstances with only belief degrees being available, which can be described by uncertainty theory. By far, the new theory has been successfully applied to deal with many uncertain decision-making problems, e.g., option pricing [30, 31], facility location [32], portfolio selection [33], inventory problem [34], project scheduling problem [35–37], and production control problem [38]. Recently, Huang and Ke [8] applied uncertainty theory to a pricing decision problem in a supply chain with one common retailer. Besides, Chen et al.[39] studied an effort decision problem in a supply chain with one manufacturer and one retailer under uncertain information. However, both of them did not consider the pricing problem in a supply chain with competing retailers.

This paper extends the above literatures on the pricing problems with competing retailers [17–19, 28], by employing uncertainty theory to depict the costs and demands estimated by experts’ experience data in practice. Three uncertain game models are built to explore the equilibrium behaviors of the decentralized supply chain under different power structures. Meanwhile, we consider the retailers’ sales costs which are often ignored in most literatures. Then, we explore the effects of uncertain degrees of the manufacturing costs and sales costs on the equilibrium prices determined by the supply chain managers. Some interesting managerial highlights are gained from some numerical experiments conducted in this paper.

Preliminaries

Let Γ be a nonempty set and a σ-algebra over Γ. Each element Λ in is called an event.

Definition 1

([ 2 ]) The set function is called an uncertain measure if it satisfies:

Axiom 1

(Normality axiom) .

Axiom 2

(Duality axiom) for any event Λ.

Axiom 3

(Subadditivity axiom) For every countable sequence of events {Λ _i }, i=1,2,⋯, we have

Besides, the product uncertain measure on the product σ-algebra was defined by Liu [40] as follows:

Axiom 4

(Product axiom) Let be uncertainty spaces for k=1,2,⋯ The product uncertain measure is an uncertain measure satisfying where Λ _k are arbitrarily chosen events from for k=1,2,⋯, respectively.

Definition 2

([ 2 ]) An uncertain variable is a measurable function ξ from an uncertainty space to the set of real numbers, i.e., for any Borel set B of real numbers, the set

$$\{\xi\in B\}=\{\gamma\in \Gamma \ \big|\ \xi(\gamma)\in B\} $$

is an event.

Definition 3

([ 40 ]) The uncertain variables ξ ₁,ξ ₂,⋯,ξ _n are said to be independent if for any Borel sets B ₁,B ₂,⋯,B _n of real numbers.

Sometimes, we should know uncertainty distribution to model real-life uncertain optimization problems.

Definition 4

([ 2 ]) The uncertainty distribution Φ of an uncertain variable ξ is defined by for any real number x.

An uncertainty distribution Φ is referred to be regular if its inverse function Φ ⁻¹(α) exists and is unique for each α∈[0,1].

Lemma 1

([ 3 ]) Let ξ ₁,ξ ₂,⋯,ξ _n be independent uncertain variables with regular uncertainty distributions Φ ₁,Φ ₂,⋯,Φ _n , respectively. If the function f(x ₁,x ₂,⋯,x _n ) is strictly increasing with respect to x ₁,x ₂,⋯,x _m and strictly decreasing with respect to x _m+1,x _m+2,⋯,x _n , then

$$\xi=f(\xi_{1}, \xi_{2}, \cdots, \xi_{n}) $$

is an uncertain variable with inverse uncertainty distribution

$$\Phi^{-1}(\alpha)=f(\Phi_{1}^{-1}(\alpha),\cdots,\Phi_{m}^{-1}(\alpha),\Phi_{m+1}^{-1}(1-\alpha),\cdots,\Phi_{n}^{-1}(1-\alpha)). $$

Definition 5

([ 2 ]) Let ξ be an uncertain variable. The expected value of ξ is defined by provided that at least one of the above two integrals is finite.

Lemma 2

([ 3 ]) Let ξ be an uncertain variable with uncertainty distribution Φ. If the expected value exists, then

$$E[\xi]=\int_{0}^{+\infty} (1-\Phi(x))d x-\int_{-\infty}^{0} \Phi(x)d x. $$

Lemma 3

([ 3 ]) Let ξ be an uncertain variable with regular uncertainty distribution Φ. If the expected value exists, then

$$E[\xi]=\int_{0}^{1} \Phi^{-1}(\alpha)d \alpha. $$

Lemma 4

([ 41 ]) Let ξ ₁,ξ ₂,⋯,ξ _n be independent uncertain variables with regular uncertainty distributions Φ ₁,Φ ₂,⋯,Φ _n , respectively. A function f(x ₁,x ₂,⋯,x _n ) is strictly increasing with respect to x ₁,x ₂,⋯,x _m and strictly decreasing with respect to x _m+1,x _m+2,⋯,x _n . Then, the expected value of ξ=f(ξ ₁,ξ ₂,⋯,ξ _n ) is

$$ \begin{aligned} \mathrm{E}[\xi]=\int_{0}^{1} f(\Phi_{1}^{-1}(\alpha),\cdots,\Phi_{m}^{-1}(\alpha),\Phi_{m+1}^{-1}(1-\alpha),\cdots,\Phi_{n}^{-1}(1-\alpha)))\mathrm{d}\alpha \end{aligned} $$

(1)

provided that the expected value E[ξ] exists.

Example 1

Let ξ and η be two positive independent uncertain variables with regular uncertainty distributions Φ and Ψ, respectively. Then we have

$$ \begin{aligned} E\left[\frac{\xi}{\eta}\right]=\int_{0}^{1}\frac{\Phi^{-1}(\alpha)}{\Psi^{-1}(1-\alpha)}\mathrm{d}\alpha. \end{aligned} $$

(2)

Problem Description

Consider a supply chain with one common manufacturer and two competing retailers: the manufacturer supplies one common product to the two retailers, and in turn, the two retailers compete to sell the product to end consumers in the same market.

Notations and Assumptions

It is assumed that the manufacturer determines the wholesale prices (w ₁,w ₂) to the two retailers and then the two retailers choose their own markup policies r ₁ and r ₂, respectively. Note that the sales prices can be decided (p _i =w _i +r _i , i=1,2) when the corresponding wholesale prices and retailer markup policies are determined. Consistent with the extant literatures [6 , 17 – 19 , 42], we suppose that each retailer faces the following linear demand function:

$$q_{i}=d_{i}-\beta p_{i}+\gamma p_{3-i},\ i=1,2 $$

where d _i represents the potential market size of retailer i, β is the self-price elasticity coefficient, γ is the cross-price elasticity coefficient, and p _i is the sales price of retailer i. Note that γ/β denotes the substitutability of the two retailers.

Owing to the complicated and changeable environment, the manufacturing cost $\tilde {c}$, sales costs $(\tilde {s}_{1},\tilde {s}_{2})$, market sizes $(\tilde {d}_{1},\tilde {d}_{2})$, and price elasticity coefficients $\tilde {\beta },\tilde {\gamma }$ are usually unknown to the supply chain managers. Thus, belief degrees, given by experienced experts, are often employed to estimate these parameters due to the lack of historical data. To sum up, we give the notations shown in Table 1.

Table 1 Notations

Note that some basic concepts and theorems of uncertainty theory are provided in the “Preliminaries” section. Interested readers can consult Liu [1] for more details of the uncertainty theory. In order to attain closed-form solutions, some necessary assumptions are made as follows:

• As each retailer’s demand should be more sensitive to changes of its own price than to changes of the other retailer, it is assumed that the elasticity coefficients $\tilde {\beta }$ and $\tilde {\gamma }$ satisfy: $\mathrm {E}[\tilde {\beta }]>\mathrm {E}[\tilde {\gamma }]>0$.

• All the uncertain coefficients are assumed nonnegative and mutually independent.

• All the supply chain members have access to the same information on the demands and the costs.

• All the supply chain members are risk neutral.

• All the pricing activities are assumed to be completed in a cycle.

• The wholesale prices and markups should exceed the costs and the retailers’ demands are always positive:

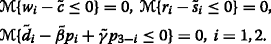
Crisp Forms of Objective Functions

In order to derive the equilibrium solutions, we transform uncertain objective functions to equivalent crisp forms first. Let $\tilde {c}, \tilde {s}_{i}, \tilde {d}_{i}, \tilde {\beta }$, and $\tilde {\gamma }$ be positive independent uncertain variables with regular uncertainty distributions Φ _c , $\Phi _{s_{i}},\Phi _{d_{i}}$, Φ _β , and Φ _γ , i=1,2.

As , one can find that π _m is monotone increasing function of $\tilde {d}_{i}$, $\tilde {\gamma }$ and monotone decreasing with $\tilde {c}$, $\tilde {\beta }$, and $\tilde {s}_{i}$. Thus, referring to Lemma 4, the expected object function of the manufacturer can be attained as follows:

$$ \begin{aligned} \pi_{m} &=\sum\limits_{i=1}^{2}E\left[\left(w_{i}-\tilde{c}_{i}\right)\left(\tilde{d}_{i}-\tilde{\beta} \left(r_{i}+w_{i}\right)+ \tilde{\gamma} \left(r_{3-i}+w_{3-i}\right)\right)\right]\\ &=\sum\limits_{i=1}^{2}\int_{0}^{1}\left[\left(w_{i}-\Phi_{c}^{-1}(1-\alpha)\right)\left(\Phi_{d_{i}}^{-1}(\alpha)-\Phi_{\beta}^{-1}(1-\alpha) \left(r_{i}+w_{i}\right)\right.\right.\\ &\left.\left.\quad+\Phi_{\gamma}^{-1}(\alpha)\left(r_{3-i}+w_{3-i}\right)\right)\right] {\mathrm{d}} \alpha. \end{aligned} $$

(3)

Define

$$ \begin{aligned} E&[\tilde{a}^{1-\alpha} \tilde{b}^{\alpha}]=\int_{0}^{1}\Phi_{a}^{-1}(1-\alpha)\Phi_{b}^{-1}(\alpha)\mathrm{d} \alpha,\\ E&[\tilde{a}^{1-\alpha} \tilde{b}^{1-\alpha}]=\int_{0}^{1}\Phi_{a}^{-1}(1-\alpha)\Phi_{b}^{-1}(1-\alpha)\mathrm{d} \alpha. \end{aligned} $$

(4)

where $\Phi _{a}^{-1}$ and $\Phi _{b}^{-1}$ are the inverse distribution functions of $\tilde {a}$ and $\tilde {b}$, respectively.

Then, the crisp form of π _m can be attained as follows:

$$ \begin{aligned} \pi_{m} =&\sum\limits_{i=1}^{2}\int_{0}^{1}[(w_{i}-\Phi_{c}^{-1}(1-\alpha))(\Phi_{d_{i}}^{-1}(\alpha)-\Phi_{\beta}^{-1}(1-\alpha) (r_{i}+w_{i})\\ &+\Phi_{\gamma}^{-1}(\alpha)(r_{3-i}+w_{3-i}))]\mathrm{d} \alpha\\ =&\sum\limits_{i=1}^{2}\{-\mathrm{E}[\tilde{\beta}] w_{i}^{2}+\mathrm{E}[\tilde{\gamma}] w_{3-i}w_{i}+(-\mathrm{E}[\tilde{\beta}] r_{i}+ \mathrm{E}[\tilde{\gamma}] r_{3-i}+E[\tilde{d}_{i}]+E[\tilde{c}_{i}^{1-\alpha}\tilde{\beta}^{1-\alpha}]) w_{i}\\ \ & -E[\tilde{c}^{1-\alpha} \tilde{d}_{i}^{\alpha}]+E[\tilde{c}^{1-\alpha} \tilde{\beta}^{1-\alpha}] r_{i} - E[\tilde{c}^{1-\alpha} \tilde{\gamma}^{\alpha}](r_{3-i}+w_{3-i})\}. \end{aligned} $$

(5)

Similarly, the crisp forms of the expected profit functions of the retailers can also be attained as follows:

$$ \begin{aligned} \pi_{r_{i}} =&-E[\tilde{\beta}] r_{i}^{2}+E[\tilde{\gamma}]r_{3-i}r_{i}+(-E[\tilde{\beta}] w_{i}+ E[\tilde{\gamma}] w_{3-i}+E[\tilde{d}_{i}]+E[\tilde{s}_{i}^{1-\alpha}\tilde{\beta}^{1-\alpha}]) r_{i}\\ \ & -E[\tilde{s}_{i}^{1-\alpha} \tilde{d}_{i}^{\alpha}]+E[\tilde{s}_{i}^{1-\alpha} \tilde{\beta}^{1-\alpha}] w_{i} - E[\tilde{s}_{i}^{1-\alpha} \tilde{\gamma}^{\alpha}](r_{3-i}+w_{3-i}),\ i=1,2. \end{aligned} $$

(6)

Models and Solution Approaches

In this section, starting with the Manufacturer Stackelberg (MS) model, we present the general formulations and solutions to three types of supply chain pricing models with different power structures.

MS Model

In the first case, we assume that the manufacturer plays a dominant role and announces its wholesale prices (w ₁,w ₂) to maximize its own profit allowing for the retailers’ reaction functions. Observing the wholesale prices, the two retailers noncooperatively choose their own markup pricing schemes r _i to maximize their own profits conditional on the other retailer’s decision. Then, the retail prices are decided as well as the ordering quantities. Thus, a Stackelberg-Nash game can be applied as follows:

To solve this Stackelberg-Nash game model, opposite to the decision sequence, we should first derive the Nash equilibrium at the lower level for the given wholesale prices w ₁ and w ₂ specified by the manufacturer in advance.

Proposition 1

Given the wholesale prices (w ₁,w ₂), the Nash equilibrium in the lower level can be obtained as follows:

$$ \begin{aligned} r_{1}(w_{1},w_{2})=&\frac{-2E[\tilde{\beta}]^{2}+E[\tilde{\gamma}]^{2}}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}w_{1}+\frac{E[\tilde{\beta}]E[\tilde{\gamma}] }{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}w_{2} \\&+\frac{2E[\tilde{\beta}](E[\tilde{d}_{1}]+ E[\tilde{\beta}^{1-\alpha}\tilde{s}_{1}^{1-\alpha}])+E[\tilde{\gamma}](E[\tilde{d}_{2}]+E[\tilde{\beta}^{1-\alpha}\tilde{s}_{2}^{1-\alpha}])}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}},\\ r_{2}(w_{1},w_{2})=&\frac{-2E[\tilde{\beta}]^{2}+E[\tilde{\gamma}]^{2}}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}w_{2}+\frac{E[\tilde{\beta}]E[\tilde{\gamma}] }{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}w_{1}\\& +\frac{2E[\tilde{\beta}](E[\tilde{d}_{2}]+ E[\tilde{\beta}^{1-\alpha}\tilde{s}_{2}^{1-\alpha}])+E[\tilde{\gamma}](E[(\tilde{d}_{1}]+E[\tilde{\beta}^{1-\alpha}\tilde{s}_{1}^{1-\alpha}])}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}.\\ \end{aligned} $$

(7)

Proof

Referring to the two retailers’ expected objective functions with the given wholesale prices, we can get

$$ \begin{aligned} \frac {\partial^{2}\pi_{r_{1}}}{\partial r_{1}^{2}}=-2E[\tilde{\beta}]<0,\ \frac {\partial^{2}\pi_{r_{2}}}{\partial r_{2}^{2}}=-2E[\tilde{\beta}]<0, \end{aligned} $$

(8)

with the assumption $E[\tilde {\beta }]>E[\tilde {\gamma }]>0$. Hence, $\pi _{r_{1}}$ and $\pi _{r_{2}}$ are concave in r ₁ and r ₂, respectively. Setting the first-order derivatives equaling zero, we have

$$ \begin{aligned} \frac {\partial \pi_{r_{1}}}{\partial r_{1}}=&-2E[\tilde{\beta}] r_{1}+E[\tilde{\gamma}]r_{2}-E[\tilde{\beta}] w_{1}+ E[\tilde{\gamma}] w_{2}+E[\tilde{d}_{1}]+E[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}]=0, \\ \frac {\partial \pi_{r_{2}}}{\partial r_{2}}=&-2E[\tilde{\beta}] r_{2}+E[\tilde{\gamma}]r_{1}-E[\tilde{\beta}] w_{2}+ E[\tilde{\gamma}] w_{1}+E[\tilde{d}_{2}]+E[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}]=0. \end{aligned} $$

(9)

The followers’ optimal responses to (w ₁,w ₂) can be easily obtained by solving the above two equations as follows:

$$ \begin{aligned} r_{1}^{*}(w_{1},w_{2})=&\frac{-2E[\tilde{\beta}]^{2}+E[\tilde{\gamma}]^{2}}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}w_{1}+\frac{E[\tilde{\beta}]E[\tilde{\gamma}] }{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}w_{2} \\&+\frac{2E[\tilde{\beta}](E[\tilde{d}_{1}]+ E[\tilde{\beta}^{1-\alpha}\tilde{s}_{1}^{1-\alpha}])+E[\tilde{\gamma}](E[\tilde{d}_{2}]+E[\tilde{\beta}^{1-\alpha}\tilde{s}_{2}^{1-\alpha}])}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}},\\ r_{2}^{*}(w_{1},w_{2})=&\frac{-2E[\tilde{\beta}]^{2}+E[\tilde{\gamma}]^{2}}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}w_{2}+\frac{E[\tilde{\beta}]E[\tilde{\gamma}] }{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}w_{1}\\& +\frac{2E[\tilde{\beta}](E[\tilde{d}_{2}]+ E[\tilde{\beta}^{1-\alpha}\tilde{s}_{2}^{1-\alpha}])+E[\tilde{\gamma}](E[(\tilde{d}_{1}]+E[\tilde{\beta}^{1-\alpha}\tilde{s}_{1}^{1-\alpha}])}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}}.\\ \end{aligned} $$

(10)

Thus, Proposition 1 is proved. □

The manufacturer, given the optimal responses of the two retailers, will make decisions to maximize its expected profit.

Proposition 2

Given the optimal responses of the two retailers, we can obtain the following:(1) π _m is jointly concave with respect to w ₁ and w ₂;(2) The optimal decisions of the manufacturer are as follows:

$$ \begin{aligned} &w_{1}^{*}= \frac{A(E[\tilde{d}_{1}]-E[\tilde{\beta}]S_{1}+E[\tilde{\gamma}]S_{2}+C)+B(E[\tilde{d}_{2}]-E[\tilde{\beta}]S_{2}+E[\tilde{\gamma}]S_{1}+C)} {2(A^{2}-B^{2})},\\ &w_{2}^{*}=\frac {A(E[\tilde{d}_{2}]-E[\tilde{\beta}]S_{2}+E[\tilde{\gamma}]S_{1}+C)+B(E[\tilde{d}_{1}]-E[\tilde{\beta}]S_{1}+E[\tilde{\gamma}]S_{2}+C)} {2(A^{2}-B^{2})} \end{aligned} $$

(11)

where

$$\begin{aligned} &A=\frac{2E[\tilde{\beta}]^{3}-E[\tilde{\beta}]E[\tilde{\gamma}]^{2}}{4E[\tilde{\beta}]^{2}-E[ \tilde{\gamma}]^{2}}, \ B=\frac{E[\tilde{\beta}]^{2}E[\tilde{\gamma}]}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}},\\ &C=\frac{(2E[\tilde{\beta}]^{2} +E[\tilde{\beta}]E[\tilde{\gamma}])(E[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}]- E[\tilde{c^{1-\alpha}}\tilde{\gamma}^{\alpha}])}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}},\\ &S_{i}=\frac{2E[\tilde{\beta}](E[\tilde{d}_{i}]+ E[\tilde{\beta}^{1-\alpha}\tilde{s}_{i}^{1-\alpha}])+E[\tilde{\gamma}](E[\tilde{d}_{3-i}]+E[\tilde{\beta}^{1-\alpha}\tilde{s}_{3-i}^{1-\alpha}])}{4E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2}},\ i=1,2.\\ \end{aligned} $$

Proof

Substituting the two retailers’ reaction functions Eqs‘. (7) into the manufacturer’s profit function, and we obtain

$$ \begin{aligned} \pi_{m}=&\sum\limits_{i=1}^{2}E[(w_{i}-\tilde{c})(\tilde{d}_{i}-\tilde{\beta}(r_{i}^{*}+w_{i})+\tilde{\gamma}(r_{i}^{*}+w_{i}))]\\ =&\sum\limits_{i=1}^{2}E[(w_{i}-\tilde{c})(\tilde{d}_{i}-\tilde{\beta}(\frac{2E[\tilde{\beta}]^{2}}{4E[\tilde{\beta}]^{2} -E[\tilde{\gamma}]^{2}} w_{i}+\frac{E[\tilde{\beta}]E[\tilde{\gamma}]}{4E[\tilde{\beta}]^{2} -E[\tilde{\gamma}]^{2}}w_{3-i}+S_{i})\\ &+\tilde{\gamma}(\frac{2E[\tilde{\beta}]^{2}}{4E[\tilde{\beta}]^{2} -E[\tilde{\gamma}]^{2}} w_{3-i}+\frac{E[\tilde{\beta}]E[\tilde{\gamma}]}{4E[\tilde{\beta}]^{2} -E[\tilde{\gamma}]^{2}}w_{i}+S_{3-i}))]\\ =&\sum\limits_{i=1}^{2}\{E[\tilde{d}_{i}]w_{i}-A w_{i}^{2}+B w_{3-i}w_{i}-E[\tilde{\beta}]S_{i}w_{i}+E[\tilde{\gamma}]S_{3-i}w_{i} \\&-E[\tilde{c}^{1-\alpha}\tilde{d}_{i}^{\alpha}]+E[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}]S_{i} -E[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}]S_{3-i}\\ &+\frac{2E[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}]E[\tilde{\beta}]^{2}-E[\tilde{\beta}]E[\tilde{\gamma}]E[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}]}{4E[\tilde{\beta}]^{2} -E[\tilde{\gamma}]^{2}} w_{i}\\ &+\frac{E[\tilde{\beta}]E[\tilde{\gamma}]E[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}]-2E[\tilde{\beta}]^{2}E[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}]}{4E[\tilde{\beta}]^{2} -E[\tilde{\gamma}]^{2}}w_{3-i}\}. \end{aligned} $$

(12)

Referring to Eq. (12), we can obtain the Hessian matrix with the corresponding second-order derivatives of the objective function π _m as follows:

$$H= \left|\begin{array}{ll} \frac {\partial^{2}\pi_{m}}{\partial w_{1}^{2}}&\frac {\partial^{2}\pi_{m}}{\partial w_{1}\partial w_{2}}\\ \frac {\partial^{2}\pi_{m}}{\partial w_{2}\partial w_{1}} &\frac {\partial^{2}\pi_{m}}{\partial w_{2}^{2}}\\ \end{array}\right| = \left|\begin{array}{ll} -2A& 2B\\ 2B& -2A \end{array}\right| $$

With assumption $E[\tilde {\beta }]>E[\tilde {\gamma }]>0$, we can obtain

$$A=\frac{2E[\tilde{\beta}]^{3}-E[\tilde{\beta}]E[\tilde{\gamma}]^{2}}{4E[\tilde{\beta}]^{2}-E[ \tilde{\gamma}]^{2}}> \frac{E[\tilde{\beta}]^{3}}{4E[\tilde{\beta}]^{2}-E[ \tilde{\gamma}]^{2}}>\frac{E[\tilde{\beta}]^{2}E[\tilde{\gamma}]}{4E[\tilde{\beta}]^{2}-E[ \tilde{\gamma}]^{2}}=B. $$

It can be easily seen that H is negative definite and π _m is jointly concave with respect to w ₁ and w ₂. Therefore, differentiating π _m by (w ₁,w ₂) and equating the expressions to zero, we have

$$\begin{aligned} \frac {\partial\pi_{m}(w_{1},w_{2})}{\partial w_{1}}=-2{Aw}_{1}+2{Bw}_{2}+E[\tilde{d}_{1}]-E[\tilde{\beta}]S_{1}+E[\tilde{\gamma}]S_{2}+C=0,\\ \frac {\partial\pi_{m}(w_{1},w_{2})}{\partial w_{2}}=-2{Aw}_{2}+2{Bw}_{1}+E[\tilde{d}_{2}]-E[\tilde{\beta}]S_{2}+E[\tilde{\gamma}]S_{1}+C=0, \end{aligned} $$

and the leader’s equilibrium prices (w ₁,w ₂) can be easily obtained by solving the above two equations

$$ \begin{aligned} &w_{1}^{*}= \frac{A(E[\tilde{d}_{1}]-E[\tilde{\beta}]S_{1}+E[\tilde{\gamma}]S_{2}+C)+B(E[\tilde{d}_{2}]-E[\tilde{\beta}]S_{2}+E[\tilde{\gamma}]S_{1}+C)} {2(A^{2}-B^{2})},\\ &w_{2}^{*}=\frac {A(E[\tilde{d}_{2}]-E[\tilde{\beta}]S_{2}+E[\tilde{\gamma}]S_{1}+C)+B(E[\tilde{d}_{1}]-E[\tilde{\beta}]S_{1}+E[\tilde{\gamma}]S_{2}+C)} {2(A^{2}-B^{2})}. \end{aligned} $$

(13)

Thus, Proposition 2 is proved. □

Based on Propositions 1 and 2, we can get the equilibrium prices of the two retailers as follows:

$$\begin{aligned} r_{1}^{*}=&\frac{\left(-2E\left[\tilde{\beta}\right]^{2}+E\left[\tilde{\gamma}\right]^{2}\right) w_{1}^{*}+E\left[\tilde{\beta}\right]E\left[\tilde{\gamma}\right] w_{2}^{*}+2E\left[\tilde{\beta}\right]\left(E\left[\tilde{d}_{1}\right]+ E\left[\tilde{\beta}\tilde{s}_{1}\right]\right)}{4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &+\frac{E\left[\tilde{\gamma}\right]\left(E\left[\tilde{d}_{2}\right]+E\left[\tilde{\beta}\tilde{s}_{2}\right]\right)}{4E\left[\tilde{\beta}\right]^{2} -E\left[\tilde{\gamma}\right]^{2}},\\ r_{2}^{*}=&\frac{\left(-2E\left[\tilde{\beta}\right]^{2}+E\left[\tilde{\gamma}\right]^{2}\right)w_{2}^{*}+E\left[\tilde{\beta}\right]E\left[\tilde{\gamma}\right] w_{1}^{*}+2E\left[\tilde{\beta}\right]\left(E\left[\tilde{d}_{2}\right]+ E\left[\tilde{\beta}\tilde{s}_{2}\right]\right)}{4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &+\frac{E\left[\tilde{\gamma}\right]\left(E\left[\tilde{d}_{1}\right]+E\left[\tilde{\beta}\tilde{s}_{1}\right] \right)}{4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}. \end{aligned} $$

RS Model

The second possible structure is that the manufacturer distributes its products through two supper retailers which are much bigger than the manufacturer. We assume that the two retailers can dominate the sales prices by choosing their markup policies firstly. Then, a Nash-Stackberg model can be applied as follows:

Similarly, opposite to the decision sequence, we should derive the follower’s response to the given retail markups r ₁ and r ₂ specified by the two retailers.

Proposition 3

Observing the two retailers’ retail markups r ₁ and r ₂, the manufacturer’s optimal response is:

$$ {\begin{aligned} w_{1}(r_{1},r_{2})=\frac{E[\tilde{\beta}]E[\tilde{d_{1}}]+E[\tilde{\gamma}]E[\tilde{d_{2}}]+ (E[\tilde{\beta}]+E[\tilde{\gamma}])(E[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}]-E[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}])}{2(E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2})}-\frac{1}{2}r_{1},\\ w_{2}(r_{1},r_{2})=\frac{E[\tilde{\beta}]E[\tilde{d_{2}}]+E[\tilde{\gamma}]E[\tilde{d_{1}}]+ (E[\tilde{\beta}]+E[\tilde{\gamma}])(E[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}]-E[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}])}{2(E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2})}-\frac{1}{2}r_{2}.\\ \end{aligned}} $$

(14)

Proof

Referring to Eq.(5), the Hessian matrix with the corresponding second-order derivatives of the equivalent objective function π _m can be attained:

$$H_{2}= \left|\begin{array}{ll} \frac {\partial^{2}\pi_{m}}{\partial w_{1}^{2}}&\frac {\partial^{2}\pi_{m}}{\partial w_{1}\partial w_{2}}\\ \frac {\partial^{2}\pi_{m}}{\partial w_{2}\partial w_{1}} &\frac {\partial^{2}\pi_{m}}{\partial w_{2}^{2}}\\ \end{array}\right| = \left|\begin{array}{ll} -2E[\tilde{\beta}]& 2E[\tilde{\gamma}]\\ 2E[\tilde{\gamma}]& -2E[\tilde{\beta}] \end{array}\right| $$

Obviously, the Hessian matrix is negative definite with the assumption $E[\tilde {\beta }]> E[\tilde {\gamma }]> 0$. Then, the optimal reaction functions to (r ₁,r ₂) can be derived from the first-order conditions.

$$ { \begin{aligned} \frac {\partial\pi_{m}}{\partial w_{1}}=&-2E\left[\tilde{\beta}\right]w_{1}+2E\left[\tilde{\gamma}\right]w_{2}+E\left[\tilde{d}_{1}\right]-E\left[\tilde{\beta}\right]r_{1}+E\left[\tilde{\gamma}\right]r_{2}+E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\\ &-E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]=0,\\ \frac {\partial\pi_{m}}{\partial w_{2}}=&-2E\left[\tilde{\beta}\right]w_{2}+2E\left[\tilde{\gamma}\right]w_{1}+E\left[\tilde{d}_{2}\right]-E\left[\tilde{\beta}\right]r_{2}+E\left[\tilde{\gamma}\right]r_{1}+E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\\ &-E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]=0. \end{aligned}} $$

(15)

By solving Eqs. (15), we can obtain:

$$ {\begin{aligned} w_{1}(r_{1},r_{2})=\frac{E[\tilde{\beta}]E[\tilde{d_{1}}]+E[\tilde{\gamma}]E[\tilde{d_{2}}]+ (E[\tilde{\beta}]+E[\tilde{\gamma}])(E[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}]-E[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}])}{2(E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2})}-\frac{1}{2}r_{1},\\ w_{2}(r_{1},r_{2})=\frac{E[\tilde{\beta}]E[\tilde{d_{2}}]+E[\tilde{\gamma}]E[\tilde{d_{1}}]+ (E[\tilde{\beta}]+E[\tilde{\gamma}])(E[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}]-E[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}])}{2(E[\tilde{\beta}]^{2}-E[\tilde{\gamma}]^{2})}-\frac{1}{2}r_{2}.\\ \end{aligned}} $$

(16)

Thus, Proposition 3 is proved. □

Given the manufacturer’s response, the two retailers compete to choose their own sales markups.

Proposition 4

The Nash equilibrium between the two retailers is as follows:

$$ \begin{aligned} r_{1}^{*}=&\frac{2E\left[\tilde{\beta}\right]E\left[\tilde{d_{1}}\right]+E\left[\tilde{\gamma}\right]E\left[\tilde{d_{2}}\right]- \left(2E\left[\tilde{\beta}\right]+E\left[\tilde{\gamma}\right]\right)E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]-E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]} {4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &+\frac{2E\left[\tilde{\beta}\right]E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]+E\left[\tilde{\gamma}\right]E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] }{4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}},\\ r_{2}^{*}=&\frac{2E\left[\tilde{\beta}\right]E\left[\tilde{d_{2}}\right]+E\left[\tilde{\gamma}\right]E\left[\tilde{d_{1}}\right]- \left(2E\left[\tilde{\beta}\right]+E\left[\tilde{\gamma}\right]\right)E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]-E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]} {4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &+\frac{2E\left[\tilde{\beta}\right]E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]+E\left[\tilde{\gamma}\right]E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] }{4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}. \end{aligned} $$

(17)

Proof

Substituting Eqs. (14) into the two retailers’ profit functions, we obtain:

$$ { \begin{aligned} \pi_{r_{1}}=&-\frac{1}{2}E\left[\tilde{\beta}\right]r_{1}^{2}+\frac{1}{2}E\left[\tilde{\gamma}\right]r_{2}r_{1}+\frac{1}{2} \left(E\left[\tilde{d_{1}}\right]-E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]+E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]\right.\\ &\left.+E\left[s_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)r_{1} -E\left[\tilde{s}_{1}^{1-\alpha}\tilde{d}_{1}^{\alpha}\right]+E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] D_{1}-E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]\left(D_{2}+\frac{1}{2}r_{2}\right),\\ \pi_{r_{2}}=&-\frac{1}{2}E\left[\tilde{\beta}\right]r_{2}^{2}+\frac{1}{2}E\left[\tilde{\gamma}\right]r_{1}r_{2}+\frac{1}{2} \left(E\left[\tilde{d_{2}}\right]-E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]+E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]\right.\\ &\left.+E\left[s_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)r_{1} -E\left[\tilde{s}_{2}^{1-\alpha}\tilde{d}_{2}^{\alpha}\right]+E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] D_{2}-E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]\left(D_{1}+\frac{1}{2}r_{1}\right)\\ \end{aligned}} $$

(18)

where

$$ {\begin{aligned} D_{i}=\frac{E\left[\tilde{\beta}\right]E\left[\tilde{d_{i}}\right]+E\left[\tilde{\gamma}\right]E\left[\tilde{d_{3-i}}\right]+ \left(E\left[\tilde{\beta}\right]+E\left[\tilde{\gamma}\right]\right)\left(E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] -E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right] \right)}{2\left(E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}\right)},\ i=1,2. \end{aligned}} $$

(19)

With the second-order condition $\frac {\partial ^{2}\pi _{r_{i}}}{\partial r_{i}^{2}}=-E[\tilde {\beta }]<0$, the first-order conditions can be shown as follows:

$$ {\begin{aligned} \frac {\partial\pi_{r_{1}}}{\partial r_{1}}=&-E\left[\tilde{\beta}\right]r_{1}+\frac{1}{2}E\left[\tilde{\gamma}\right]r_{2}+\frac{1}{2} \left(E\left[\tilde{d_{1}}\right]-E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] +E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]+E\left[s_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)=0,\\ \frac {\partial\pi_{r_{2}}}{\partial r_{2}}=&-E\left[\tilde{\beta}\right]r_{2}+\frac{1}{2}E\left[\tilde{\gamma}\right]r_{1}+\frac{1}{2} \left(E\left[\tilde{d_{2}}\right]-E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] +E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]+E\left[s_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)=0. \end{aligned}} $$

(20)

By solving Eq. (20), the optimal decisions of the two retailers can be derived:

$$ \begin{aligned} r_{1}^{*}=&\frac{2E\left[\tilde{\beta}\right]E\left[\tilde{d_{1}}\right]+E\left[\tilde{\gamma}\right]E\left[\tilde{d_{2}}\right]- \left(2E\left[\tilde{\beta}\right]+E\left[\tilde{\gamma}\right]\right)E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] -E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]} {4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &+\frac{2E\left[\tilde{\beta}\right]E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] +E\left[\tilde{\gamma}\right]E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] }{4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}},\\ r_{2}^{*}=&\frac{2E\left[\tilde{\beta}\right]E\left[\tilde{d_{2}}\right]+E\left[\tilde{\gamma}\right]E\left[\tilde{d_{1}}\right]- \left(2E\left[\tilde{\beta}\right]+E\left[\tilde{\gamma}\right]\right)E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] -E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]} {4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &+\frac{2E\left[\tilde{\beta}\right]E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] +E\left[\tilde{\gamma}\right]E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] }{4E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}. \end{aligned} $$

(21)

Thus, Proposition 4 is proved. □

Based on Propositions 3 and 4, we can get the equilibrium prices of the manufacturer as follows:

$$ {\begin{aligned} w_{1}^{*}=\frac{E\left[\tilde{\beta}\right]E\left[\tilde{d_{1}}\right]+E\left[\tilde{\gamma}\right]E\left[\tilde{d_{2}}\right]+ \left(E\left[\tilde{\beta}\right]+E\left[\tilde{\gamma}\right]\right)\left(E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] -E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]\right)}{2\left(E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}\right)} -\frac{1}{2}r_{1}^{*},\\ w_{2}^{*}=\frac{E\left[\tilde{\beta}\right]E\left[\tilde{d_{2}}\right]+E\left[\tilde{\gamma}\right]E\left[\tilde{d_{1}}\right]+ \left(E\left[\tilde{\beta}\right]+E\left[\tilde{\gamma}\right]\right)\left(E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right] -E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]\right)}{2\left(E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}\right)} -\frac{1}{2}r_{2}^{*}.\\ \end{aligned}} $$

(22)

VN Model

In some supply chains, there is no obvious dominance between chain members. In this case, we assume that the three players move simultaneously. Then, a three-player Nash game model can be built as follows:

Proposition 5

In the Nash equilibrium of the three-player game, the equilibrium prices are obtained as follows:

$$ { \begin{aligned} r_{1}^{*}=&\frac{\left.\left(-6E\left[\tilde{\beta}\right]^{2}+2E\left[\tilde{\gamma}\right]^{2}\right)D_{1} +4E\left[\tilde{\beta}\right]E\left[\tilde{\gamma}\right]D_{2}+6E\left[\tilde{\beta}\right]\left(E\left[\tilde{d}_{1}\right]+ E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)\right)}{9E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &+\frac{2E\left[\tilde{\gamma}\right]\left(E\left[\tilde{d}_{2}\right]+E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)} {9E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}},\\ r_{2}^{*}=&\frac{\left(-6E\left[\tilde{\beta}\right]^{2}+2E\left[\tilde{\gamma}\right]^{2}\right)D_{2}+4E\left[\tilde{\beta}\right]E\left[\tilde{\gamma}\right] D_{1}+6E\left[\tilde{\beta}\right]\left(E\left[\tilde{d}_{2}\right]+E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)} {9E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &+\frac{2E\left[\tilde{\gamma}\right]\left(E\left[\tilde{d}_{1}\right]+E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)} {9E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}},\\ w_{1}^{*}=&\frac{\left(12E\left[\tilde{\beta}\right]^{2}-2E\left[\tilde{\gamma}\right]^{2}\right)D_{1}-2E\left[\tilde{\beta}\right]E\left[\tilde{\gamma}\right] D_{2}-3E\left[\tilde{\beta}\right]\left(E\left[\tilde{d}_{1}\right]+E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)} {9E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &-\frac{E\left[\tilde{\gamma}\right]\left(E\left[\tilde{d}_{2}\right]+E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)} {9E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}},\\ w_{2}^{*}=&\frac{\left(12E\left[\tilde{\beta}\right]^{2}-2E\left[\tilde{\gamma}\right]^{2}\right)D_{2}-2E\left[\tilde{\beta}\right]E\left[\tilde{\gamma}\right] D_{1}-3E\left[\tilde{\beta}\right]\left(E\left[\tilde{d}_{2}\right]+E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)} {9E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}\\ &-\frac{E\left[\tilde{\gamma}\right]\left(E\left[\tilde{d}_{1}\right]+E\left[\tilde{s}_{1}^{1-\alpha}\tilde{\beta}^{1-\alpha}\right]\right)} {9E\left[\tilde{\beta}\right]^{2}-E\left[\tilde{\gamma}\right]^{2}}. \end{aligned}} $$

Proof

Note that π _m is jointly concave in (w ₁,w ₂) and $\pi _{r_{i}}$ is concave with respect to r _i , i=1,2. Set the first-order derivatives equaling zero as follows:

$$ \begin{aligned} \frac {\partial \pi_{m}}{\partial w_{1}}=&-2E\left[\tilde{\beta}\right] w_{1}+ 2E\left[\tilde{\gamma}\right] w_{2} -E\left[\tilde{\beta}\right] r_{1}+E\left[\tilde{\gamma}\right] r_{2}+E\left[\tilde{d}_{1}\right]+E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{\alpha}\right]\\&- E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]=0,\\ \frac {\partial \pi_{m}}{\partial w_{2}}=&-2E\left[\tilde{\beta}\right] w_{2}+ 2E\left[\tilde{\gamma}\right] w_{1} -E\left[\tilde{\beta}\right] r_{2}+E\left[\tilde{\gamma}\right] r_{1}+E\left[\tilde{d}_{2}\right]+E\left[\tilde{c}^{1-\alpha}\tilde{\beta}^{\alpha}\right]\\&- E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]=0,\\ \frac {\partial \pi_{r_{1}}}{\partial r_{1}}=&-2E\left[\tilde{\beta}\right] r_{1}+ E\left[\tilde{\gamma}\right] r_{2} -E\left[\tilde{\beta}\right] w_{1}+E\left[\tilde{\gamma}\right] w_{2}+E\left[\tilde{d}_{1}\right]+E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{\alpha}\right]=0,\\ \frac {\partial \pi_{r_{2}}}{\partial r_{2}}=&-2E\left[\tilde{\beta}\right] r_{2}+ E\left[\tilde{\gamma}\right] r_{1}-E\left[\tilde{\beta}\right] w_{2}+E\left[\tilde{\gamma}\right] w_{1}+E\left[\tilde{d}_{2}\right]+ E\left[\tilde{s}_{2}^{1-\alpha}\tilde{\beta}^{\alpha}\right]=0. \end{aligned} $$

(23)

By solving Eqs.(23), the equilibrium solutions of Eqs.(26) can be attained. □

Similarly, the sales prices, ordering quantities, and expected profits can also be attained.

Numerical Experiments

By the results obtained from the above models, the expressions of each supply chain member’s optimal decision and optimal expected profit can be easily attained. Because of the complicated forms of the equilibrium prices and expected profits, it is quite difficult (if possible) to conduct analytical comparisons to obtain general conclusions. Instead, we employ numerical approach to illustrate supply chain members’ different behaviors and performances facing various decision environments with different power structures and uncertain degrees.

When dealing with indeterminate quantities (e.g., demands and costs) without enough historical data (samples), experienced experts are usually employed to estimate these quantities in practice and hence uncertainty theory can be applied. Interested readers can consult Liu [1] (Chapter 16: Uncertain Statistics) to get more details on how to collect experts’ experimental data and how to estimate empirical distribution of uncertain variable from the experimental data. For simplicity, we just list uncertainty distributions of the uncertain parameters in Table 2.

Table 2 Distributions of uncertain variables

Additionally, this paper uses $E[\tilde {\gamma }]/E[\tilde {\beta }]$ to represent the substitutability of the two retailers. Let $\tilde {\beta }$ remain constant and vary $\tilde {\gamma }$ at three levels, we show the data in Table 3.

Table 3 Substitutability of the two retailers

With Lemma 3, we can attain $E[\tilde {c}]=(9+11)/2=10, \ E[\tilde {s}_{1}]=(5+7)/2=6$, $E[\tilde {s}_{2}]=(4+6)/2=5$, $E[\tilde {d}_{1}]=(2900+2\times 3000+3300)/4=3050$, $E[\tilde {d}_{2}]=(2800+2\times 3000+3100)/4=2975$, etc.

According to Lemma 4, we have

$$ \begin{aligned} E\left[\tilde{c}^{1-\alpha}\tilde{d_{1}}^{\alpha}\right]=&\int_{0}^{1}\left[\Phi_{c}^{-1}(1-\alpha)\Phi_{d_{1}}^{-1}(\alpha)\right]\mathrm{d}\alpha\\ = & \int_{0}^{0.5}(11(1-\alpha))+9\alpha)(2900 \times(1-2\alpha)+2\times3000\alpha)\mathrm{d}\alpha\\ &\ \ +\int_{0.5}^{1}(11(1-\alpha)+9\alpha)(3000\times(2-2\alpha)+3300\times(2\alpha-1))\mathrm{d}\alpha\\ =&3043.33,\\ E\left[\tilde{c}^{1-\alpha}\tilde{\gamma}^{\alpha}\right]=&\int_{0}^{1}\left[\Phi_{c}^{-1}(1-\alpha)\Phi_{\gamma}^{-1}(\alpha)\right]\mathrm{d}\alpha\\ = & \int_{0}^{1}(11(1-\alpha))+9\alpha)(40(1-\alpha)+60\alpha)\mathrm{d}\alpha\\ =& 496.67. \end{aligned} $$

(24)

In the same way, we can get the values of $E[\tilde {c}^{1-\alpha }\tilde {\beta }^{1-\alpha }]$, $E[\tilde {c}^{1-\alpha }\tilde {\gamma }^{\alpha }]$, $E[\tilde {s}_{r}^{1-\alpha }\tilde {\beta }^{1-\alpha }]$, $E[\tilde {s}_{r}^{1-\alpha }\tilde {\gamma }^{\alpha }]$, etc.

Substituting these values into the equilibrium solutions attained in the “Models and Solution Approaches” section, we can obtain Table 4.

Table 4 The equilibrium results of the three structures under different substitutability

Referring to Table 4, one can find the following:

• Regardless of the leadership, the sales prices and the expected profits of the total system in the MS and RS structures are the same, indicating that no matter who holds the power has no influence on the total supply chain. However, in consideration of the individual firms, the firm acts as a leader will gain more profit than as a follower.

• The dominant power structure will increase the sales prices and lower the profits of the whole supply chain as the sales prices in the VN case are the lowest.

Next, we analyze the effects of the uncertain degrees of the manufacturing costs and sales costs on the optimal pricing decisions under the three possible structures. The uncertain degree of a parameter mainly depends on its own inherent variance and experts’ personal knowledge. If more information on a parameter is available, more accurate estimations the experts can make. Then, as a result, the uncertain degree of the parameter will decrease. Of course, if we have enough information (historical data) on these parameters and their distributions can be precisely estimated, then we can apply probability theory rather than uncertainty theory. Note that the forms of the equilibrium solutions of these models under stochastic environment are the same to those under deterministic environment with the assumption of risk neutral members.

By varying the uncertain degrees of these parameters and keeping the other parameters unchanged as shown in Table 2, the changes of optimal prices are shown in Tables 5, 6, and 7.

Table 5 Effects of the manufacturing cost’s uncertain degree on the prices and profits

Table 6 Effects of the 1st retailer’s sales cost’s uncertain degree on the prices and profits

Table 7 Effects of the 2nd retailer’s sales cost’s uncertain degree on the prices and profits

Referring to Table 5, we obtain the following results:

• The wholesale prices will increase while the markup prices of the two retailers will drop when the uncertain degree of the manufacturing cost increases in the three structures.

• The manufacturer can benefit from the vagueness of the manufacturing costs, while the other channel members, namely the two retailers, will suffer from less profits.

• When the uncertain degree of the manufacturing cost increases, the whole supply chain will gain more, meanwhile, consumers have to pay more.

Referring to Tables 6 and 7, we obtain the following results:

• When the uncertain degree of its sales cost becomes higher, each retailer will be charged a lower wholesale price, while the wholesale price for the other retailer will keep the same in the MS structure and drop slightly in the RS and VN structures.

• Both the retailers can charge higher markup prices when the uncertain degree of either of the sales costs increases.

• Contrary to the effect of the manufacturing cost’s uncertain degree, the retailers can gain higher profits while the common manufacturer will suffer from lower profit with the increase of the uncertain degree of the sales costs.

• In the same way, when the uncertain degree of the sales costs increases, end consumers will afford higher prices while the whole supply chain will gain more.

Similarly, more experiments can be conducted to explore the effects of the other parameters, such as the two price elastic coefficients or the market sizes of the two retailers.

Conclusions

In this paper, we considered a pricing competing problem in supply chain with competing retailers. Specially, the manufacturing costs, sales costs, and consumer demands were characterized as uncertain variables. Meanwhile, three decentralized models based on uncertainty theory and game theory were built to formulate the pricing decision problems. The equilibrium behaviors of the supply chain under three possible power structures were derived from these models. Afterwards, numerical experiments were also given to explore the impacts of uncertain degrees of the parameters on the pricing decisions. The results showed that the existence of dominant power in a supply chain will increase the sales prices and lower the profits of the whole supply chain. It was also found that the supply chain members may benefit from higher uncertain degrees of their own costs, whereas the supply chain members at the other level will gain less profits. Additionally, the results demonstrated that the uncertainty of the supply chain will make end consumers pay more.

As this study was based on some assumptions, future researches can focus on some more general problems. For instance, this paper only considered one type of indeterminacy, while the real world might behave more complicated in which randomness and uncertainty might coexist. Therefore, one possible extension of this paper is to study the pricing problem with twofold indeterminacy, in which uncertain random variable can be applied. Besides, this paper assumed that all the participants are risk neutral while the decision makers may be risk sensitive in the real world. The research can be more applicable if the equilibrium behaviors with risk-sensitive members are considered.